Domaine de dérivabilité

[Youssri]

Bonsoir,
Comment déterminé la domaine de dérivabilité d'une fonction composée?
par exemple f(x) = arcsin(sin(x))

[aviateur]

BJr
la fonction sinus est dérivable sur R, la fonction arcsinus sur ]-1,1[.
donc f est dérivable pour tout x tel que
Maintenant il reste à vérifier si pour f est dérivable ou non.

[pascal16]

arcsin(sin(x)) : trace-là sous geogebra pour comprendre que la dérivée ne sert à rien


f(g)'=g'*f'(g)

[aviateur]

La dérivée sert à rien?
C'est pas la question!!

[Ben314]

Salut,
Pour mettre tout le monde d'accord, perso, j'ai tendance à penser que les deux approches sont intéressantes, c'est à dire que dans un exo. "bien fait",
1) On commence par demander la continuité puis la dérivabilité de la fonction ainsi que sa dérivée (là ou elle existe) : ça fait un très bon exercice "un peu difficile" sur les dérivées de fonction composées.
2) Puis on demande dans un deuxième temps de retrouver le résultat par du "pur calcul algébrique", ce qui fait un très bon exercice de révision de la trigonométrie (et sur les "pièges" des fonctions trigo. inverses)

Voire même une question 1.5) de "vision graphique" demandant à l'élève de tracer le graphe de f uniquement à l'aide de f(0) et des valeurs "bizarres" qu'on a trouvé pour f'(x)

[aviateur]

Il me semble évidemment qu'il faut comprendre la question dans sa généralité.
C'est à dire que pour une fonction définie sur (par exemple) par h(x)=f(g(x)).
Que dire de la dérivabilité de h en un point tel que g soit dérivable en mais f n'est pas dérivable en

L'exemple n'étant là que pour illustrer la question.
Comme par exemple f(x)=|sin(x^3)| est -elle dérivable sur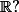 (en particulier en x=0 que se passe-t-il?
alors que | | ne l'est pas en x=0.
Ma réponse est qu'il faut faire une étude à part.

[pascal16]

en regardant de plus près, il y a un peu de travail.

par exemple : surtout ne pas dire f(x)=x sans préciser sur quel domaine

et avant la dérivabilité, pour la continuité, je ne vois pas comment faire l'impasse sur de la trigo qui donne toutes les réponses

la fonction dérivée de la composée est cool (c'est toujours au programme ?)