Domaine de définition et de dérivabilité d'une fonction

[IbraK64]

Bonjour, je souhaite d'or et déjà remercier toute personne qui lira ce message et qui y répondra. J'ai une petite question sur un exercice de dérivation d'une fonction.

Voici l'énoncé: f(x) = x^2 + (ln(x+3)) / ln(x^2+6x+9)
Question : Quel est le domaine de définition et de dérivabilité de la fonction ?

Ma réponse : f(x) = x^2 + (ln(x+3)) / ln(x^2+6x+9) = x^2 + (ln(x+3)) / ln((x+3)^2) = x^2 + (ln(x+3)) / 2ln(x+3) = x^2 + 1/2

La question que je me pose maintenant c'est est-ce que je dois définir le domaine de définition et de dérivabilité de f(x) = x^2 + (ln(x+3)) / ln(x^2+6x+9) ou de f(x) = x^2 + 1/2.
En effet, si je le définis avec f(x) = x^2 + (ln(x+3)) / ln(x^2+6x+9) alors la fonction f est dérivable pour x appartenant à ]-3;-2[ U ]-2;+infini[ , mais si je le définis avec f(x) = x^2 + 1/2 alors la fonction f est dérivable pour tout x réel.

Voila je ne sais pas si je dois définir le domaine de définition et de dérivabilité de la fonction de base ou bien de la fonction simplifiée. Merci de m'éclaircir à ce sujet afin que je ne fasse pas l'erreur de choisir la mauvaise expression lorsque je tomberai sur un exercice comme celui-ci, à moins que les deux domaines soient valables, ce qui m'étonnerais toutefois.

[catamat]

Bonjour

De façon générale l'ensemble de définition se recherche à partir de l'expression donnée dans l'énoncé donc sans transformation, surtout pas de simplification ...

Donc ici on a 3 conditions, deux provenant des logarithmes et une du dénominateur.

Pour la dérivabilité les conditions sont les mêmes dans ce cas.

[hdci]

Bonjour,

Bonjour, je souhaite d'ores et déjà remercier toute personne qui lira ce message et qui y répondra. J'ai une petite question sur un exercice de dérivation d'une fonction.

Voici l'énoncé: f(x) = x^2 + (ln(x+3)) / ln(x^2+6x+9)
Question : Quel est le domaine de définition et de dérivabilité de la fonction ?

Ma réponse : f(x) = x^2 + (ln(x+3)) / ln(x^2+6x+9) = x^2 + (ln(x+3)) / ln((x+3)^2) = x^2 + (ln(x+3)) / 2ln(x+3) = x^2 + 1/2
[...]
En effet, si je le définis avec f(x) = x^2 + (ln(x+3)) / ln(x^2+6x+9) alors la fonction f est dérivable pour x appartenant à ]-3;-2[ U ]-2;+infini[ , mais si je le définis avec f(x) = x^2 + 1/2 alors la fonction f est dérivable pour tout x réel.

Vous n'avez pas à prendre d'hypothèses simplificatrice. Par exemple la fonction définie par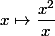 n'est pas définie en zéro, car on n'a pas le droit de diviser par zéro. Même si on voit que partout ailleurs on a f(x)=x. (Si vous avez vu la continuité, vous pouvez alors dire que la fonction est prolongeable par continuité en zéro, mais en l'état elle n'est pas définie en zéro).

Ici, c'est encore pire : ne peut pas se calculer pour x=-4 par exemple... Vous ne pouvez simplifier que si vous avez des nombres, et le logarithme de -1 n'est sûrement pas un nombre réel.

... Donc vous devez rester avec les logarithmes au numérateur et au dénominateur et considérer que le logarithme n'est défini que pour des nombres strictement positifs et les fractions pour des dénominateurs non nuls

[IbraK64]

Bonjour

De façon générale l'ensemble de définition se recherche à partir de l'expression donnée dans l'énoncé donc sans transformation, surtout pas de simplification ...

Donc ici on a 3 conditions, deux provenant des logarithmes et une du dénominateur.

Pour la dérivabilité les conditions sont les mêmes dans ce cas.

Merci pour votre réponse catamat, donc je dois définir le domaine de définition et de dérivabilité à partir de l'expression de base de la fonction f. C'est vrai que d'un point de vue logique, il faut se référer à ce qu'on nous donne comme expression de base dans un exercice. Bonne soirée à vous et encore merci pour votre réponse.

[IbraK64]

Bonjour,

Bonjour, je souhaite d'ores et déjà remercier toute personne qui lira ce message et qui y répondra. J'ai une petite question sur un exercice de dérivation d'une fonction.

Voici l'énoncé: f(x) = x^2 + (ln(x+3)) / ln(x^2+6x+9)
Question : Quel est le domaine de définition et de dérivabilité de la fonction ?

Ma réponse : f(x) = x^2 + (ln(x+3)) / ln(x^2+6x+9) = x^2 + (ln(x+3)) / ln((x+3)^2) = x^2 + (ln(x+3)) / 2ln(x+3) = x^2 + 1/2
[...]
En effet, si je le définis avec f(x) = x^2 + (ln(x+3)) / ln(x^2+6x+9) alors la fonction f est dérivable pour x appartenant à ]-3;-2[ U ]-2;+infini[ , mais si je le définis avec f(x) = x^2 + 1/2 alors la fonction f est dérivable pour tout x réel.

Vous n'avez pas à prendre d'hypothèses simplificatrice. Par exemple la fonction définie par n'est pas définie en zéro, car on n'a pas le droit de diviser par zéro. Même si on voit que partout ailleurs on a f(x)=x. (Si vous avez vu la continuité, vous pouvez alors dire que la fonction est prolongeable par continuité en zéro, mais en l'état elle n'est pas définie en zéro).

Ici, c'est encore pire : ne peut pas se calculer pour x=-4 par exemple... Vous ne pouvez simplifier que si vous avez des nombres, et le logarithme de -1 n'est sûrement pas un nombre réel.

... Donc vous devez rester avec les logarithmes au numérateur et au dénominateur et considérer que le logarithme n'est défini que pour des nombres strictement positifs et les fractions pour des dénominateurs non nuls

Merci d'avoir répondu à ma question hdci. Donc je dois bien utiliser l'expression de f donnée dans l'énoncé pour définir le domaine de définition et de dérivabilité de cette fonction.
J'aurais par ailleurs une autre question : dois-je donc ne pas utiliser l'expression simplifiée de f pour calculer la dérivée de cette fonction , dérivée avec laquelle je vais devoir dire si la fonction possède un maximum ou un minimum ?

[hdci]

Une fois le domaine de définition établi, vous pouvez faire toutes les simplifications que vous voulez. Donc oui bien sûr utilisez la forme simplifiée pour déterminer la dérivée.

Vous pouvez si vous en avez le temps faire l'exercice avec la forme non simplifiée et vérifier que vous obtenez bien le même résultat

(Par exemple, si , la fonction est égale à 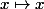sur 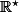et la dérivée est clairement sur l'ensemble de définition , et si vous utilisez la formule u/v, vous obtenez

[IbraK64]

Une fois le domaine de définition établi, vous pouvez faire toutes les simplifications que vous voulez. Donc oui bien sûr utilisez la forme simplifiée pour déterminer la dérivée.

Vous pouvez si vous en avez le temps faire l'exercice avec la forme non simplifiée et vérifier que vous obtenez bien le même résultat

(Par exemple, si , la fonction est égale à sur et la dérivée est clairement sur l'ensemble de définition , et si vous utilisez la formule u/v, vous obtenez

Bonsoir, il se trouve qu'en attendant votre message j'ai calculé la dérivée de f avec la formule de base ainsi que la formule simplifiée et je trouve bien la même chose.
Merci pour votre aide, je saurai pour l'avenir qu'il faut déterminer le domaine de définition et de dérivabilité d'une fonction avec l'expression de base. Bonne soirée à vous.