Simplification
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
charlotte29
- Membre Naturel
- Messages: 28
- Enregistré le: 03 Nov 2018, 17:49
-
 par charlotte29 » 03 Nov 2018, 18:01
par charlotte29 » 03 Nov 2018, 18:01
Bonsoir,
Afin de démonter qu'une suite est géométrique j'ai effectué Wn+1 sur Wn mais je n'arrive pas a simplifier mon resultat pour trouver la raison, pourriez vous m'aider svp ?
Mon résultat est 3Un-1 sur Un+1 sur 2Un-4 sur Un+1 sur Un-1 sur Un-2
Merci d'avance

-
hdci
- Membre Irrationnel
- Messages: 1962
- Enregistré le: 23 Juin 2018, 16:13
-
 par hdci » 03 Nov 2018, 18:02
par hdci » 03 Nov 2018, 18:02
Bonsoir,
Mais c'est quoi la définition de la suite ?
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
-
charlotte29
- Membre Naturel
- Messages: 28
- Enregistré le: 03 Nov 2018, 17:49
-
 par charlotte29 » 03 Nov 2018, 18:08
par charlotte29 » 03 Nov 2018, 18:08
Un+1 est définie par 4Un-2 sur Un+1 ( ou -2 et 1 ne sont pas en indices)
Wn est définie par Un-1 sur Un-2 ou -1 et -2 ne sont pas en indices
Voilà

-
hdci
- Membre Irrationnel
- Messages: 1962
- Enregistré le: 23 Juin 2018, 16:13
-
 par hdci » 03 Nov 2018, 18:39
par hdci » 03 Nov 2018, 18:39
Ok alors pour l'écriture :

Ou bien

(De l'importance des parenthèses...)
Je suppose que c'est la seconde écriture et que

Que trouves-tu pour

?
Au passage a-stu pensé à vérifier qu'on ne divise pas par 0 ? (il manque la valeur initiale

en particulier)
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
-
charlotte29
- Membre Naturel
- Messages: 28
- Enregistré le: 03 Nov 2018, 17:49
-
 par charlotte29 » 03 Nov 2018, 18:42
par charlotte29 » 03 Nov 2018, 18:42
Oui pardon, en effet c'est la seconde écriture!
Pour Wn+1 sur Wn je trouve 3Un-1 sur Un+1 sur 2Un-4 sur Un+1 sur Un-1 sur Un-2
Oui j'ai vérifié qu'on ne divise pas par 0 dans la question qui précède celle -ci !
-
pascal16
- Membre Légendaire
- Messages: 6663
- Enregistré le: 01 Mar 2017, 12:58
- Localisation: Angoulème : Ville de la BD et du FFA. gare TGV
-
 par pascal16 » 03 Nov 2018, 18:49
par pascal16 » 03 Nov 2018, 18:49
des parenthèses pour les fractions stp
tu écris simplement W(n+1) / W(n)
en haut et en bas, tu multiplies par Un+1, ça enlève une série de fractions
ça se simplifie en haut, ça se simplifie en bas
Modifié en dernier par
pascal16 le 03 Nov 2018, 18:54, modifié 1 fois.
-
hdci
- Membre Irrationnel
- Messages: 1962
- Enregistré le: 23 Juin 2018, 16:13
-
 par hdci » 03 Nov 2018, 18:51
par hdci » 03 Nov 2018, 18:51
Je ne comprends pas ton résultat, car il y a une succession de "sur" (donc de division), et-ce qu'il faut les faire dans cet ordre ?
Cela donnerait, si j'appelle q le rapport (et parce qu'en l'abscence de parenthèses on effectue les opérations de la gauche vers la droite)
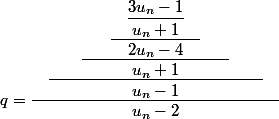
Mais je ne pense pas que ce soit cela...
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
-
charlotte29
- Membre Naturel
- Messages: 28
- Enregistré le: 03 Nov 2018, 17:49
-
 par charlotte29 » 03 Nov 2018, 18:58
par charlotte29 » 03 Nov 2018, 18:58
Oui c'est cela que je trouve comme résultat, mais j'ai du louper une simplification au début ou autre ..
-
hdci
- Membre Irrationnel
- Messages: 1962
- Enregistré le: 23 Juin 2018, 16:13
-
 par hdci » 03 Nov 2018, 19:04
par hdci » 03 Nov 2018, 19:04
Je ne pense pas que ce soit le résultat, quoi qu'il en soit vu la tête de la fraction je n'ai même pas envie de la réduire.
Tu as

Donc

Ne pas tout faire d'un seul coup c'est trop compliqué et c'est là qu'on se prend les pieds dans le tapis.
Connaissant

en fonction de

, quelle est la forme la plus simple pour

?
Même question pour

.
Ecris les deux résultats en factorisant au maximum, puis calcul le rapport

avec ces fractions : tout va bien se simplifier.
Modifié en dernier par
hdci le 03 Nov 2018, 19:19, modifié 1 fois.
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
-
charlotte29
- Membre Naturel
- Messages: 28
- Enregistré le: 03 Nov 2018, 17:49
-
 par charlotte29 » 03 Nov 2018, 19:13
par charlotte29 » 03 Nov 2018, 19:13
Désolé je ne comprend vraiment pas les suites donc je ne vois pas ce que peux donner Un+1 -1 et Un+1 - 2

-
hdci
- Membre Irrationnel
- Messages: 1962
- Enregistré le: 23 Juin 2018, 16:13
-
 par hdci » 03 Nov 2018, 19:19
par hdci » 03 Nov 2018, 19:19
Par définition :

Donc

Une somme faisant intervenir des fractions se fait en mettant au même dénominateur (ce n'est pas une question de "ne rien comprendre aux suites", c'est une question "d'appliquer des résultats de collège" : il ne faut pas paniquer ou se buter contre de nouvelles notions, on ne fait qu'utiliser ce qu'on connaît déjà).
}{u_n+1}=\dfrac{3u_n-3}{u_n+1}=3\dfrac{u_n-1}{u_n+1})
Fais de même avec

Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
-
charlotte29
- Membre Naturel
- Messages: 28
- Enregistré le: 03 Nov 2018, 17:49
-
 par charlotte29 » 03 Nov 2018, 19:24
par charlotte29 » 03 Nov 2018, 19:24
Pour Un+1 - 2 je trouve (2Un-4) / Un+1
-
hdci
- Membre Irrationnel
- Messages: 1962
- Enregistré le: 23 Juin 2018, 16:13
-
 par hdci » 03 Nov 2018, 19:29
par hdci » 03 Nov 2018, 19:29
charlotte29 a écrit:Pour Un+1 - 2 je trouve (2Un-4) / (Un+1)
J'ai ajouté les parenthèses manquantes !
C'est cela, mais tu peux factoriser par 2, fais-le (pourquoi ? Parce qu'en général les formes factorisée ont le bon goût d'être plus simples et finalement de se simplifier, ce que tu verras quand tu fera le rapport

Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
-
charlotte29
- Membre Naturel
- Messages: 28
- Enregistré le: 03 Nov 2018, 17:49
-
 par charlotte29 » 03 Nov 2018, 19:35
par charlotte29 » 03 Nov 2018, 19:35
En factorisant par 2 j'arrive à 2 ((Un-2) / (Un+1))
-
hdci
- Membre Irrationnel
- Messages: 1962
- Enregistré le: 23 Juin 2018, 16:13
-
 par hdci » 03 Nov 2018, 19:44
par hdci » 03 Nov 2018, 19:44
OK.
On revient maintenant à
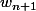
: pour rappel

Tu as calculé:
- le numérateur :

- et le dénominateur

Que vaut donc
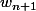
?
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
-
charlotte29
- Membre Naturel
- Messages: 28
- Enregistré le: 03 Nov 2018, 17:49
-
 par charlotte29 » 03 Nov 2018, 19:48
par charlotte29 » 03 Nov 2018, 19:48
Selon moi on arriverait à (3Un-1)/ (2Un-2) ?
-
hdci
- Membre Irrationnel
- Messages: 1962
- Enregistré le: 23 Juin 2018, 16:13
-
 par hdci » 03 Nov 2018, 19:56
par hdci » 03 Nov 2018, 19:56
Tu as correctement simplifié les
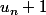
.
Mais tu fais une autre erreur. Pourquoi le 3 qui est en facteur dans

, viendrait tout-à-coup se développer au numérateur sur

et pas sur le

? Tu devrais trouver

(mais voir la dernière remarque ci-dessous)
Même chose pour le 2 du dénominateur.
Mais justement, le fait de mettre en facteur, ce n'est pas pour redévelopper après (sinon ça ne sert à rien). Conserve les facteurs et ré-écrit le résultat (tu y es presque).
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
-
charlotte29
- Membre Naturel
- Messages: 28
- Enregistré le: 03 Nov 2018, 17:49
-
 par charlotte29 » 03 Nov 2018, 20:00
par charlotte29 » 03 Nov 2018, 20:00
Oui c'est vrai qu'en réfléchissant ça ne paraît pas logique de mettre le 3 devant le Un et ne pas le multiplier par -1 . Donc je dirais qu'on peut mettre des parenthèses ce qui nous donnerait 3(Un-1) / 2(Un-2) ?
-
hdci
- Membre Irrationnel
- Messages: 1962
- Enregistré le: 23 Juin 2018, 16:13
-
 par hdci » 03 Nov 2018, 20:04
par hdci » 03 Nov 2018, 20:04
Voilà, c'est cela !
Maintenant, mets le 3/2 en facteur et tu obtiens :

La seconde fraction ne te rappelle rien (voir la définition de
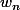
)
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
-
charlotte29
- Membre Naturel
- Messages: 28
- Enregistré le: 03 Nov 2018, 17:49
-
 par charlotte29 » 03 Nov 2018, 20:06
par charlotte29 » 03 Nov 2018, 20:06
Donc si je comprend bien, (Un-1) / (Un-2) correspond à Wn donc Wn+1 = 3/2 x Wn et donc ma suite est bien géométrique de raison 3/2 ?

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités

