Espaces vectoriel

[mamine]

Bonjour, je souhaiterai savoir par la methode du determinant si deux vecteurs de R^2 ou trois vecteurs de R^3 sont libre ou lié. Si après calcul du determinant je le trouve nul, cela veux dire que les vecteurs sont-ils libres ou lié ? Si le determinant est non nul cela veux ils que les vecteurs sont libre ou lié ? Merci pour votre aide.

[hdci]

Bonjour,

Il y a bien un lien entre la nullité du déterminant et la liberté (ou non) du système.
Plutôt que de vous donner la réponse, je vous donne moyen simple de retrouver le résultat : si l'un des vecteurs est nul :

• le système est-il libre ou lié ?
• quelle est la valeur du déterminant ?

[mamine]

Je crois que si l'un des vecteurs est nul alors le système est libre et le determinant sera aussi égal à zéro ?

[FLBP]

Salut,

donc et ne sont pas libres.
Et le déterminant vaut 0.
Une autre manière de voire les choses, est que le déterminant de deux vecteurs dans le plan, donne l'aire du parallélogramme formé par ces derniers. (Et dans l'espace le déterminant vaut le volume du tétraèdre)
Si les vecteurs sont linéairement dépendant, le parallélogramme en 2d sera une ligne -> aire 0 et le tétraèdre plat, car les vecteur sont coplanaire : volume 0.

[sylvainc22]

Autre facon de l'expliquer pour des vecteurs de où au moins b n'est pas nul.
Si a et b sont proportionnels alors il existe une constante k telle que a=kb c'est à dire




et comme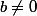 l'équation formelle suivante est toujours vraie: Donc s'il existe bel et bien une valeur numérique de k telle que alors les deux équations 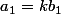et sont vérifiées et a et b sont proportionnels ou liés. Si une telle valeur de k n'existe pas les équations ne sont pas vérifiées et a et b sont indépendants.