Espaces vectoriel normé
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
 par legeniedesalpages » 19 Mar 2008, 01:25
par legeniedesalpages » 19 Mar 2008, 01:25
E#Mc² a écrit: legeniedesalpages a écrit:
Il y a un theoreme qui classifie ou reduit la theorie des espace hilbertiens, en gros, il dit que tout espace hilbertien (je dis bien hilbertien, pas infini qcq) est isomorphe à l², tu peux regarder le livre de Claude wagshal : Integration , pour enoncé exact .(c'est une excellente reference pour le sujet) j'ai pas compris ce que t'as pas compris pour ta version algebrqiue, attention pour la IR comme Q-ev, c'est pas possible de la construire une base , ca existe ! ca a l air deroutant!! :marteau:
ok je chercherai ce bouquin à la bu pour plus de compléments.

Donc on peut pas expliciter une base, l'existence est due au lemme de Zorn alors(extension du théorème de la base incomplète dans le cas de la dimension infinie).
 par alavacommejetepousse » 19 Mar 2008, 09:35
par alavacommejetepousse » 19 Mar 2008, 09:35
E#Mc² a écrit:
Il y a un theoreme qui classifie ou reduit la theorie des espace hilbertiens, en gros, il dit que tout espace hilbertien (je dis bien hilbertien, pas infini qcq) est isomorphe à l², :
mon dernier message n était pas pour toi mais pour legéniedesalpages
pour cet isomorphisme il faut bien préciser hilbert séparable.
 par legeniedesalpages » 19 Mar 2008, 10:59
par legeniedesalpages » 19 Mar 2008, 10:59
alavacommejetepousse a écrit:mon dernier message n était pas pour toi mais pour legéniedesalpages
pour cet isomorphisme il faut bien préciser hilbert séparable.
je ne vois pas où il y a une erreur dans mon post #4 ? :hein:
 par legeniedesalpages » 19 Mar 2008, 12:58
par legeniedesalpages » 19 Mar 2008, 12:58
On suppose que

et que
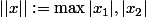)
pour tout
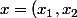\in \mathbb{R}^2)
.
Soient
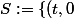\in E:\ t\in [0,1]\})
(resp.
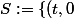\in E:\ t\in \mathbb{R}\})
) et
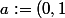)
.
Justifier que

est convexe fermé et déterminer les points de

réalisant la distance de

au sous-ensemble

. Le résultat obtenu est-il en contradiction avec le théorème d'existence et d'unicité de la projection sur un convexe fermé non vide d'un espace de Hilbert.
J'ai montré dans les deux cas que S est un convexe fermé.
Ensuite, on cherche donc les points
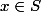
tels que
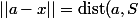)
,
ie
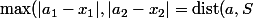)
,
et par définition
=\inf_{y\in S}\ ||y-a|| = \inf_{y\in S}\ \max(|y_1-a_1|,|y_2-a_2|)=\inf_{y\in S}\ \max(|y_1-a_1|,|a_2|))
,
mais je ne vois pas comment les déterminer.

-
E#Mc²
- Membre Naturel
- Messages: 26
- Enregistré le: 18 Mar 2008, 22:40
-
 par E#Mc² » 19 Mar 2008, 14:13
par E#Mc² » 19 Mar 2008, 14:13
legeniedesalpages a écrit:On suppose que

et que
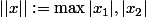)
pour tout
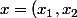\in \mathbb{R}^2)
.
Soient
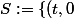\in E:\ t\in [0,1]\})
(resp.
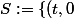\in E:\ t\in \mathbb{R}\})
) et
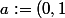)
.
Justifier que

est convexe fermé et déterminer les points de

réalisant la distance de

au sous-ensemble

. Le résultat obtenu est-il en contradiction avec le théorème d'existence et d'unicité de la projection sur un convexe fermé non vide d'un espace de Hilbert.
J'ai montré dans les deux cas que S est un convexe fermé.
Ensuite, on cherche donc les points
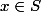
tels que
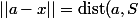)
,
ie
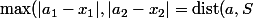)
,
et par définition
=\inf_{y\in S}\ ||y-a|| = \inf_{y\in S}\ \max(|y_1-a_1|,|y_2-a_2|)=\inf_{y\in S}\ \max(|y_1-a_1|,|a_2|))
,
mais je ne vois pas comment les déterminer.

Remarque, que d(a,S) est superieure a 1, (puisque a_{2}=1), cela te donne une idée sur la valeur de d(a,S) .... dans les deux cas tu trouves que les points a determiner est egal au premier ensemble S .
 par legeniedesalpages » 23 Mar 2008, 00:46
par legeniedesalpages » 23 Mar 2008, 00:46
E#Mc² a écrit:Remarque, que d(a,S) est superieure a 1, (puisque a_{2}=1), cela te donne une idée sur la valeur de d(a,S) .... dans les deux cas tu trouves que les points a determiner est egal au premier ensemble S .
ah oui, je devais être fatigué :mur:
je suis d'accord, juste que dans le deuxième cas, je trouve que la distance est atteinte par les éléments de
\in E:\ t\in [-1,1]\})
.
Merci.
 par legeniedesalpages » 23 Mar 2008, 00:50
par legeniedesalpages » 23 Mar 2008, 00:50
Le résultat obtenu est-il en contradiction avec le théorème d'existence et d'unicité de la projection sur un convexe fermé non vide d'un espace de Hilbert.
Je pense que non, car ici la norme n'est pas induite par un produit scalaire.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités
