Espaces vectoriel normé

[legeniedesalpages]

Bonsoir,

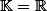
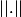
Soient un -espace vectoriel de dimension finie ( ou ), une norme sur et un fermé non vide de , et un élément de .

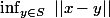
Je ne vois pas comment montrer que la borne inférieure est atteinte.

Merci pour votre aide.

[E#Mc²]

Bonsoir,

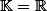
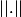
Soient un -espace vectoriel de dimension finie ( ou ), une norme sur et un fermé non vide de , et un élément de .

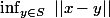
Je ne vois pas comment montrer que la borne inférieure est atteinte.

Merci pour votre aide.

Facile , il suffit de se rappeler du theorme suivant, vrai en dimesion finie : si E e.v.n de dimension finie, alors tout fermé borné est compact . A toi de deduire la suite ...

[alavacommejetepousse]

bonsoir

l'intersection de S avec une boule bien choisie est un compact

pas assez rapide

[legeniedesalpages]

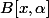
ok je prends une boule compacte avec , son intersection avec est un compact non vide et, définie sur ,
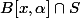
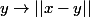
l'application y atteint son infimum qui n'est autre que .

Merci.

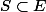
Dans le cas où est de dimension infinie, peut-on avoir des fermés tels que la distance ne soit pas atteinte pour certains ?

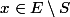
Edit: Peut être comme ça c'est plus clair, z est une variable muette pour définir le nombre

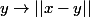
c'est une application,

(le 'y' qui est pas en latex c'est du français)

[alavacommejetepousse]

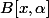
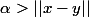
ok je prends une boule compacte avec , son intersection avec est un compact non vide et, définie sur ,
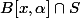
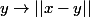
l'application y atteint son infimum qui n'est autre que .

[/TEX]?

heu qui est y ?

[E#Mc²]

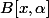
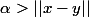
ok je prends une boule compacte avec , son intersection avec est un compact non vide et, définie sur ,
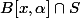
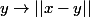
l'application y atteint son infimum qui n'est autre que .

Merci.

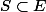
Dans le cas où est de dimension infinie, peut-on avoir des fermés tels que la distance ne soit pas atteinte pour certains ?

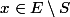
C'est pas vrai en dimension infinie, une generalisation de cette propritié en dimension infinie utilise les espaces de Hilbert... qui resemblent aux espaces de dimension finie, mais c'est faux en general, y des contre exemples, :++:

[legeniedesalpages]

C'est pas vrai en dimension infinie, une generalisation de cette propritié en dimension infinie utilise les espaces de Hilbert... qui resemblent aux espaces de dimension finie, mais c'est faux en general, y des contre exemples, :++:

Justement en fait, je suis en train de lire ça dans mon cours d'analyse hilbertienne, c'est juste avant de parler du théorème d'existence et unicité de la projection sur un convexe fermé d'un espace de Hilbert.

Mais je ne vois pas a priori un tel contre-exemple.

[E#Mc²]

Justement en fait, je suis en train de lire ça dans mon cours d'analyse hilbertienne, c'est juste avant de parler du théorème d'existence et unicité de la projection sur un convexe fermé d'un espace de Hilbert.

Mais je ne vois pas a priori un tel exemple.

Je crois que c'est pas facile d avoir un contre exemple, ca demande du temps, tu pourras penser a l espace des suites muni d une norme adequate, l 'espace des fonctions L^{2} integrables ....

[legeniedesalpages]

Je crois que c'est pas facile d avoir un contre exemple, ca demande du temps, tu pourras penser a l espace des suites muni d une norme adequate, l 'espace des fonctions L^{2} integrables ....

l'espace des suites ?

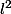
[E#Mc²]

:id:

l'espace des suites ?

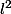
tu parles de norme l² pour les suites? si c'est le cas, c'est un hilbertien, secret :id: l'espace des fonctions reelles qui sont L² integrables , resemble a l espace des suites l², c'est la meme chose .

[legeniedesalpages]

Bon je chercherai ça en étudiant ces structures j'ai quelques exos sur ces structures.

Il y a quelque chose que j'ai pas trouvé très clair.

Le prof compte nous construire des bases de Hilbert orthonormale dénombrable sur ces espaces, qui ne seraient pas des "bases algébriques" car on a besoin en plus d'une topologie pour utiliser des limites pour les définir.

Il me semble que l'une des conséquences du lemme de Baire et que tout Banach de dimension infinie est de dimension non dénombrable.

Il y aurait donc une différence entre ces deux notions de base, mais je ne vois pas laquelle.

[legeniedesalpages]

:id:


tu parles de norme l² pour les suites? si c'est le cas, c'est un hilbertien, secret :id: l'espace des fonctions reelles qui sont L² integrables , resemble a l espace des suites l², c'est la meme chose .

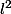
oui on a construit aujourd'hui à la main, et aussi avec la mesure discrète sur les entiers, tout juste.

[E#Mc²]

Bon je chercherai ça en étudiant ces structures j'ai quelques exos sur ces structures.

Il y a quelque chose que j'ai pas trouvé très clair.

Le prof compte nous construire des bases de Hilbert orthonormale dénombrable sur ces espaces, qui ne seraient pas des "bases algébriques" car on a besoin en plus d'une topologie pour utiliser des limites pour les définir.

Il me semble que l'une des conséquences du lemme de Baire et que tout Banach de dimension infinie est de dimension non dénombrable.

Il y aurait donc une différence entre ces deux notions de base, mais je ne vois pas laquelle.

:marteau: J'ai pas de reponses maintenant, mais tu pourras faire une analogie (meme c'est un peu loin ) avec la construction des nombres réels a partir des rationnels , IR est bien un Banach, je ne sais pas si cela seras eclairant;??! :ptdr:

[alavacommejetepousse]

il ne faut pas en effet confondre une base hilbertienne et une base algébrique

un vecteur se decompose suivant une INFINITE de vecteurs de la base hilbertienne ( dénombrable) (il est somme d une série convergente )

alors que ds une base algébrique
un vecteur est cbl d 'un nombre fini de vecteurs de la base.

tu n as pas lu ma remarque? ta preuve ne va pas

[E#Mc²]

il ne faut pas en effet confondre une base hilbertienne et une base algébrique

un vecteur se decompose suivant une INFINITE de vecteurs de la base hilbertienne ( dénombrable) (il est somme d une série convergente )

alors que ds une base algébrique
un vecteur est cbl d 'un nombre fini de vecteurs de la base.

tu n as pas lu ma remarque? ta preuve ne va pas

mon dernier message, n etait pas une preuve . j'ai juste voulu t'inviter a faire la comparaison, remarque que tout reel peut etre ecrire comme vecteur qui se decompose en une serie infini, si tu te rappelles de la construction des réels comme suites de cauchy... c'est juste une analogie . je connais pas le sujet, ou plutot ca fait des années que j ai pas fais analyse, je suis plus algebriste :zen:

[legeniedesalpages]

il ne faut pas en effet confondre une base hilbertienne et une base algébrique

un vecteur se decompose suivant une INFINITE de vecteurs de la base hilbertienne ( dénombrable) (il est somme d une série convergente )

alors que ds une base algébrique
un vecteur est cbl d 'un nombre fini de vecteurs de la base.

tu n as pas lu ma remarque? ta preuve ne va pas

ah oui voilà c'est ce que je ne saisissais pas au niveau des bases, suite à ta remarque de ton post #5, j'ai modif le psot #4 au lieu d'en faire un nouveau ( :marteau: ), c'est vrai que j'avais mis des y un peu trop partout, malgré ces modif ça ne va toujours pas? :hein:

[legeniedesalpages]

mon dernier message, n etait pas une preuve . j'ai juste voulu t'inviter a faire la comparaison, remarque que tout reel peut etre ecrire comme vecteur qui se decompose en une serie infini, si tu te rappelles de la construction des réels comme suites de cauchy... c'est juste une analogie . je connais pas le sujet, ou plutot ca fait des années que j ai pas fais analyse, je suis plus algebriste :zen:

euh oui avec le développement décimal, je vois comment écrire naturellement avec une série infinie "rationnelle" un réel.

C'est quoi en fait la définition de la base algébrique pour des ev de dimension finie?
est une base de si , et si toute famillle finie de est linéairement indépendante, c'est bien ça?

[E#Mc²]

[quote="legeniedesalpages"]euh oui avec le développement décimal, je vois comment écrire naturellement avec une série infinie "rationnelle" un réel.

C'est quoi en fait la définition de la base algébrique pour des ev de dimension finie?
est une base de si , et si toute famillle finie de est linéairement indépendante, c'est bien ça?[/QUOT

Def: Soit E un e.v. de dimension finie, on appelle base de E toute famille generatrice (ou libre) de cardinal la dimension de l espace.

On parle de base algebrique en dimesion finie, bien si on suppose que l espace est normé . en plus une base "algebrique" coincide " avec "base hilbertienne " , c'est trivial, ton espace est deja un Banach .

[legeniedesalpages]

euh oui avec le développement décimal, je vois comment écrire naturellement avec une série infinie "rationnelle" un réel.

C'est quoi en fait la définition de la base algébrique pour des ev de dimension finie?
est une base de si , et si toute famillle finie de est linéairement indépendante, c'est bien ça?[/QUOT

Def: Soit E un e.v. de dimension finie, on appelle base de E toute famille generatrice (ou libre) de cardinal la dimension de l espace.

On parle de base algebrique en dimesion finie, bien si on suppose que l espace est normé . en plus une base "algebrique" coincide " avec "base hilbertienne " , c'est trivial, ton espace est deja un Banach .

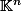
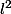
pour le cas fini je me représente à peu près, c'est pour le cas infini, j'ai du mal mais hier le prof nous a dit que l'espace de base en dimension finie c'est et pour le cas infini.

Pour le cas infini "version algébrique", je comprends mal l'idée de base, par exemple si on considère comme un -espace vectoriel, quelle base a't'on de IR?

[E#Mc²]

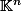
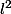
pour le cas fini je me représente à peu près, c'est pour le cas infini, j'ai du mal mais hier le prof nous a dit que l'espace de base en dimension finie c'est et pour le cas infini.

Pour le cas infini "version algébrique", je comprends mal l'idée de base, par exemple si on considère comme un -espace vectoriel, quelle base a't'on de IR?

Il y a un theoreme qui classifie ou reduit la theorie des espace hilbertiens, en gros, il dit que tout espace hilbertien (je dis bien hilbertien, pas infini qcq) est isomorphe à l², tu peux regarder le livre de Claude wagshal : Integration , pour enoncé exact .(c'est une excellente reference pour le sujet) j'ai pas compris ce que t'as pas compris pour ta version algebrqiue, attention pour la IR comme Q-ev, c'est pas possible de la construire une base , ca existe ! ca a l air deroutant!! :marteau: