Séries et inégalités maths sup analyse

[caithana]

bonjour,
je bloque à cette question de maths j'ai réussi les deux avant je vous réécrit l'énoncé

pour n dans N, on pose Sn= \sum_{k=0}^{n}\frac{(-1)^k}{2k+1} ; un= S2n et vn=S2n+1

dans la première question j'ai montré que un et vn sont adjacentes.
J'en ai déduis que Sn est convergente.

Maintenant on note S sa somme .

on me demande:
-démontrer que , pour tout n dans N, vn\le S\le un. en déduire une valeur approchée de S à 10^-3 près

je pensais chercher un DL à l'ordre 2 pour avoir f(x) - DL ordre 2équivalent à quelque chose de positif ou de négatif et si c'est positif la courbe représentative de la suite passe au dessus de l'asymptote et donc la suite est toujours au dessus de sa limite sinon c'est l'inverse.
Mai je n'arrive pas à arranger ma somme pour en faire un DL et je ne suis pas sûre de mon idée.
Merci

[caithana]

Pardon les caractères sont mal passés.

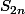pour n dans N, on pose Sn= ; un= et=

dans la première question j'ai montré que un et vn sont adjacentes.
J'en ai déduis que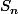 est convergente.

Maintenant on note S sa somme .

on me demande:
-démontrer que , pour tout n dans N, S . en déduire une valeur approchée de S à 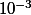près

[Ben314]

Salut,
Y'a un truc qui m'échappe un peu : quand tu dit que "tu as démontré que les suites étaient adjacentes", en fait, tu as démontré quoi concernant les deux suites ?

[caithana]

on m'a demandé de démontrer que un et vn forment un couple de suites adjacentes.

[Ben314]

Certes, certes, mais c'est quoi des suites adjacentes ?
Parce que là, le résultat qu'on te demande de montrer, ben il découle immédiatement de la définition de ce que sont des "suites adjacentes".

[caithana]

Ah oui merci!!