Probabilité

[Rayanne]

Bonsoir,
je bloque à la question 2 de ce sujet:

Code: Tout sélectionner

Le joueur A est muni d'une pièce et le joueur B d’un dés, qu’ils jettent à tour de rôle. Le joueur A gagne la partie s’il amène Face avant que B n’amène un 5 ou un 6,
et inversement. On suppose que c’est A qui commence.
1) Quelle est la probabilités de gain de A ? Celle de B ?
2) Soit T la durée de la partie.  Calculer P(T= 1),  P(T= 2), et plus généralement P(T=k). Quelle est sa durée moyenne ?

1) P(A) = 1/2
P(B) = 2/6 = 1/3

2) C'est une loi exponentielle?

Merci d'avance pour votre aide.

[aviateur]

Bonjour
La réponse 1 semble logique. Je n'ai pas fait les calculs mais 1/2+1/3 ça fait combien ?
Pour bien répondre à la question 2) il faut tout justifier la réponse 1.
Quel est ton raisonnement?

[aviateur]

D'ailleurs pour la question 2, une loi exponentielle correspond à une v.a " continue", alors qu'ici la variable T prend ces valeurs sur un ensemble discret.
Mais avant tout il faut tout il faut voir la question 1. Et puis intuitivement la probabilité pour que A gagne
serait bien plus grande que 1/2 puisqu'il commence en premier!

[Pseuda]

1) P(A) = 1/2
P(B) = 2/6 = 1/3

Bonjour,

Qu'appelles-tu P(A) ? Si c'est la probabilité que A gagne au 1er tour, c'est ça.
Qu'appelles-tu P(B) ? Si c'est la probabilité que B gagne au 1er tour, ce n'est pas ça : il faut que A perde d'abord pour que B puisse jouer.
Ce que tu as calculé, c'est la probabilité que B gagne sachant que A a perdu.

Puis il y a les autres tours.

[aviateur]

Evidemment, il faut comprendre que la question c'est "probabilité que A gagne à un certain moment."
Dans la réponse on doit avoir que la somme des 2 proba vaut 1. C'est pourquoi la réponse est fausse.
De plus intuitivement on doit avoir
En utilisant les notations de la deuxième question,
l'exercice se fera facilement si on calcule en distinguant le cas k pair puis le cas k impair.

[Pseuda]

Le problème, c'est que T arrive en 2ème question.

On appelle Ak l'événement "A gagne au tour k", Bk l'événement "B gagne au tour k". Pour calculer la probabilité de gain de chacun des joueurs, il faut calculer la somme des probabilités des Ak et des Bk de 1 à +l'infini. Le problème, c'est que ce n'est pas au programme de Terminale.

[aviateur]

Pour info j'ai trouvé p(A)=3/4 et p(B)=1/4.
Quant à savoir si c'est du programme de terminale il faut savoir sommer
pour la question 1
et pour la question 2.
Maintenant si ce n'est pas du programme de terminale, un enseignant peut très bien poser l'exercice sous forme d'un devoir, c'est à dire qu'il aide l'élève, à partir de ses connaissances du discret fini, à comprendre comment on passe au discret infini. Les suites géométriques étant une notion très bien connue des lycéens, cela ne devrait pas être un problème.
Mais ici, c'est vrai dès le départ je me suis posé la question à savoir si l'exercice tel quel est du niveau de terminale.

[Pseuda]

Effectivement on peut aider l'élève et il a tous les éléments pour y arriver. Ici, sans aide, cela s'appelle "une prise d'initiative", un peu brutale quand même. Je trouve pareil.

[aviateur]

Rebonjour
Remarque sur l'exo, si on pose la même question mais en remplaçant pour B 1/3 par 1/2 (c'est à dire qu'il joue aussi à pile ou face) la probabilité pour A de gagné va encore être supérieur à 1/2.
Alors la question que je me pose, dans l'exercice de départ ou modifié comme ici, peut-on trouver la réponse directement? (c'est à dire sans passer par le calcul explicite de la loi de T)

[Pseuda]

On peut faire un raisonnement : ils sont à 1/2 pour A et 1/6 pour B à chaque tour. Sachant que la probabilité totale doit être de 1 et qu'à chaque tour les probabilités sachant qu'ils ont tous les 2 perdus aux tours précédents sont les mêmes, on peut se douter que les proportions vont rester les mêmes.

Comme 1/2+1/6=2/3, on multiplie les deux probabilités par 3/2 arriver à 1, ce qui donne bien 3/4 et 1/4.

Sauf que cela n'est pas très rigoureux, et je ne parierais pas là-dessus sans un calcul exact.

[Rayanne]

Merci pour votre aide. Je trouve bien 3/4 pour P(A) en passant par les Ak avec un arbre de probabilité et la formule des probabilité totales:



(1/3)^n+1 tend vers 0 car (1/3)<1 donc P(A) = (1/2)*(3/2) = 3/4
Sachant que P(A) + P(B) = 1 ---> P(B) = 1/4.

[aviateur]

@pseuda, oui pour ton idée est intéressante, mais effectivement cela ne prouve rien. Et si on généralise en remplaçant 1/3 par n'importe quoi par exemple est-ce que ton interprétation résiste?
En fait
Donc si c'est "A gagne à l'étape 2k+1" on a

d'où en sommant sur :
(=3/4 si q=1/3)
Si on applique ton interprétation on a on retrouve bien p(A).

Plus généralement en remplaçant 1/2 par p et 1/3 par q on a

et alors
Ce qui montre que si B joue en premier (i.e p=1/3 et q=1/2) alors A et B ont la même chance de gagner.

La calcul de E(T) donne (=9/4 avec p=1/2 et q=1/3. )

[Pseuda]

Bonjour,

@Rayanne oui c'est bon.

@aviateur : oui il paraît assez évident que si les probabilités changent au 1er tour et restent sur le même schéma aux tours suivants, le raisonnement simplificateur résiste. Si B joue en premier, les probabilités de A1 et B1 sont 1/3 et 1/3, donc à l'infini, cela fait effectivement 1/2 et 1/2. Je n'ai pas fait la 2ème question.

[Ben314]

Salut,
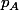
Juste une remarque : Pour calculer la proba. que A gagne à un moment ou un autre, on peut dire bêtement que, pour qu'il gagne, il faut soit qu'il gagne au premier tour (proba =1/2), soit que personne ne gagne au premier tour (proba=1/2*2/3=1/3) et qu'il gagne par la suite. Or cette proba "qu'il gagne par la suite", c'est à dire la proba conditionnelle qu'il gagne sachant que personne n'a gagné au premier tour, c'est évidement la même que la proba de gagner tout court, c'est à dire que c'est .
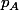
Bref, on peut se contenter d'écrire que ce qui donne puis

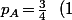Et on peut faire pareil pour l'espérance de la durée de la partie en disant qu'il y a une proba de 2/3 que la partie dure 1 tour et une proba de 1/3 quelle dure un tour de plus que l'espérance.
Donc qui donne donc

(1) En fait si on réfléchi bien, le raisonnement qu'on tient ici, c'est exactement le même que celui qu'on utilise lorsque l'on calcule en écrivant que donc en fait on "somme la série"... sans vraiment la sommer... (modulo bien entendu de savoir que la série est convergente ce qui est évident ici dans le cadre des proba.)
(2) Même remarque concernant le fait que ce qu'on fait, au fond, ça consiste à dire que, si alors (par contre, ici, sans le moindre calcul, c'est bien moins évident de dire que la série correspondant à l'espérance est convergente pour justifier le raisonnement).

[aviateur]

Bonsoir
Merci beaucoup @ben pour ta remarque qui est bien plus qu'une remarque!

[Pseuda]

Bonjour,

@Ben314. Pas mal. (je me doutais de quelque chose comme ça mais je n'ai pas osé aller jusqu'au bout).