Parallélépipède rectangle
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Macha2626
- Messages: 7
- Enregistré le: 25 Avr 2018, 14:52
-
 par Macha2626 » 25 Avr 2018, 15:00
par Macha2626 » 25 Avr 2018, 15:00
Bonjour, je dois réaliser un exercice sur le parallélépipède rectangle. Je suis en 1ère.
La consigne du sujet présente un figure avec les valeurs de certaines arrêtes de la figure. La largeur vaut x. La longueur vaut 2x. Le volume total de la figure vaut 576mm3. X varie entre 3 et 12mm.
Il s’agit d’exprimer la hauteur h en fonction de x. J’ai fait quelques essais en vain.... merci de votre aide

-
mathelot
 par mathelot » 25 Avr 2018, 15:17
par mathelot » 25 Avr 2018, 15:17
bonjour,

-
Macha2626
- Messages: 7
- Enregistré le: 25 Avr 2018, 14:52
-
 par Macha2626 » 25 Avr 2018, 16:25
par Macha2626 » 25 Avr 2018, 16:25
Oui ! C’est le résultat que j’ai trouvé mais cependant la suite de l’an question n’est pas faisable avec ce résultat.... selon moi
-
mathelot
 par mathelot » 25 Avr 2018, 16:33
par mathelot » 25 Avr 2018, 16:33
Macha2626 a écrit:Oui ! C’est le résultat que j’ai trouvé mais cependant la suite de l’an question n’est pas faisable avec ce résultat.... selon moi
quel en est l'énoncé ?
-
Macha2626
- Messages: 7
- Enregistré le: 25 Avr 2018, 14:52
-
 par Macha2626 » 25 Avr 2018, 17:13
par Macha2626 » 25 Avr 2018, 17:13
Montrer que la surface totale du parallélépipède rectangle est donnée par S(x)=(4x^3+1728)/x
La formule de la surface est bien : S=2hL+2hl+2Ll non ?
-
mathelot
 par mathelot » 25 Avr 2018, 17:22
par mathelot » 25 Avr 2018, 17:22
Macha2626 a écrit:Montrer que la surface totale du parallélépipède rectangle est donnée par S(x)=(4x^3+1728)/x
c'est la bonne formule, il n'y a pas d'erreur dans l'énoncé. A la fin du calcul,
il faut réduire
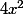
au même dénominateur x
-
Macha2626
- Messages: 7
- Enregistré le: 25 Avr 2018, 14:52
-
 par Macha2626 » 25 Avr 2018, 17:26
par Macha2626 » 25 Avr 2018, 17:26
merci beaucoup ! Je vous recontacte si je rencontre de nouvelles difficultés !

-
Macha2626
- Messages: 7
- Enregistré le: 25 Avr 2018, 14:52
-
 par Macha2626 » 26 Avr 2018, 12:58
par Macha2626 » 26 Avr 2018, 12:58
Re-bonjour,
La surface doit être égale à (4x^3+1728)/x
Cependant, je trouve (4x^2+1728)/x
Je ne comprend pas où est mon erreur...
-
mathelot
 par mathelot » 26 Avr 2018, 13:28
par mathelot » 26 Avr 2018, 13:28
Macha2626 a écrit:Cependant, je trouve (4x^2+1728)/x
.

-
Macha2626
- Messages: 7
- Enregistré le: 25 Avr 2018, 14:52
-
 par Macha2626 » 26 Avr 2018, 13:50
par Macha2626 » 26 Avr 2018, 13:50
Merci, j’ai compris maintenant... et (8x^3+1728)/x^2 est-il bien égal à (8(x-6)(x^2+6x+36))/x^2 ?
Merci !
-
mathelot
 par mathelot » 26 Avr 2018, 14:00
par mathelot » 26 Avr 2018, 14:00
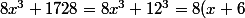(x^2-6x+36))
car
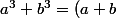(a^2-ab+b^2))
-
Macha2626
- Messages: 7
- Enregistré le: 25 Avr 2018, 14:52
-
 par Macha2626 » 26 Avr 2018, 14:05
par Macha2626 » 26 Avr 2018, 14:05
Oui ! Je vous remercie sincèrement de m’avoir aidé et d’avoir pris du temps pour m'écouter

bonne journée
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 150 invités
