Bonsoir, j'ai pas trouvé une methode pour calculer la limite de cette suite,merci de m'aider .
Un=1/n^{3}}*(\sum{k^{2}*cos(k*pi)/n})
Comment peut on savoir si elle s'agit d'une suite de riemann ou non?
Limites
6 messages
- Page 1 sur 1
Re: Limites
Un p'tit coup de balise tex :
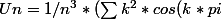/n}))
Je pense que le k pi/n a des parenthèses mal placées
avec 1/n le pas et (k/n) le point d'évaluation, on peut voir les choses comme ça :
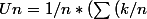^{2}*cos(pi*k/n})))
Je pense que le k pi/n a des parenthèses mal placées
avec 1/n le pas et (k/n) le point d'évaluation, on peut voir les choses comme ça :
Re: Limites
un peu ce qu'on veut, du moment que les k se suivent, on a un somme de Riemann
et puis comme ça, mira est obligé de finir lui-même, c'est pas en lisant la réponse toute faite qu'il va comprendre.
et puis comme ça, mira est obligé de finir lui-même, c'est pas en lisant la réponse toute faite qu'il va comprendre.
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
