bonjour
voici le probleme:
18x+7y=2 , determiner x et y
ma solution:
je determine une solution particuliere :
18*(3)+7*(-8)=2
en retranchant les 2 equation il vient
18(x-3)=7(-y-8)
comme 7 ne divise pas 18 alors 7 divise (x-3) d'ou
7k=x-3
x=7k+3
avec le meme raisonnement j'obtient y=-18k-8
la solution du cours:
on commence par determiner
une identite de Bezout pour les entiers 18 et 7. Pour ce faire, on utilise l'algorithme
d'Euclide, qui amene a l'identite 2*18-5*7 = 1. On en deduit la solution particuliere
x0 = 4 = 2 *2 et y0 = -10 = -5 * 2. Les entiers 7 et 18 etant premiers entre eux,
leur ppcm est egal a 7 *18 = 126 et la solution generale est donnee par x = 4+126n
et y = -10 -126n, avec n entier.
pourriez vous m'expliquer mon erreur et pourquoi une solution particuliere + ou - le ppcm suffi comme solution general ? merci
Equation diophantienne
7 messages
- Page 1 sur 1
Re: equation diophantienne
Salut,
Déjà, là où ça commence mal, c'est que et pas
et pas 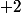 .
.
Sinon, la suite, sur le principe c'est O.K.
Déjà, là où ça commence mal, c'est que
Sinon, la suite, sur le principe c'est O.K.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: equation diophantienne
Salut,
Déjà, là où ça commence mal, c'est que et pas
et pas 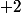 .
.
Sinon, la suite de ce que tu fait, sur le principe c'est O.K.
Par contre ça :
Déjà, là où ça commence mal, c'est que
Sinon, la suite de ce que tu fait, sur le principe c'est O.K.
Par contre ça :
C'est du grand n'importe quoi et il suffit de remplacer x par 4+126n et y par -10 -126n dans l'équation 18x+7y=2 pour voir que non seulement tu as pas toutes les solutions (le 126 est trop grand), mais même que... c'est pas des solutions de l'équation...Vlad-Drac a écrit:Les entiers 7 et 18 etant premiers entre eux,
leur ppcm est egal a 7 *18 = 126 et la solution generale est donnee par x = 4+126n
et y = -10 -126n, avec n entier.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: equation diophantienne
18 x + 7 y = 2
Déjà pour trouver la solution tu n'as pas fourni de méthode, on ne sait pas comment tu as fait.
Mettons maintenant que tu as trouvé le couple (x,y) = (a,b)
18 a + 7 b = 2
tu peux alors écrire immédiatement
18 ( a + 7k) + 7 (b - 18k) = 2
car 18*7k et 7*18k s'annulent
Ensuite, tu peux effectivement chercher si 18*7 est le ppcm de 18 et 7. Car sinon (si 18 et 7 ne sont pas premier entre eux), tu vas louper des solutions. Et donc tu as intérêt à faire cette démarche de recherche de ppcm assez tôt.
Déjà pour trouver la solution tu n'as pas fourni de méthode, on ne sait pas comment tu as fait.
Mettons maintenant que tu as trouvé le couple (x,y) = (a,b)
18 a + 7 b = 2
tu peux alors écrire immédiatement
18 ( a + 7k) + 7 (b - 18k) = 2
car 18*7k et 7*18k s'annulent
Ensuite, tu peux effectivement chercher si 18*7 est le ppcm de 18 et 7. Car sinon (si 18 et 7 ne sont pas premier entre eux), tu vas louper des solutions. Et donc tu as intérêt à faire cette démarche de recherche de ppcm assez tôt.
Re: equation diophantienne
Salut,
Pour moi, les solutions (dans Z²) de 18x + 7y = 2 sont:
x = 4 + 7k
y = -10 - 18 k
avec k dans Z

Pour moi, les solutions (dans Z²) de 18x + 7y = 2 sont:
x = 4 + 7k
y = -10 - 18 k
avec k dans Z
Re: equation diophantienne
avec le meme raisonnement j'obtient y=-18k-8
non, tu obtiens y=-18p-8 avec p dans Z, le premier k et le second k ne sont pas forcément les mêmes
ensuite tu ré-écris l'équation de départ.
tu tombes sur un truc du genre 126(k-p)=108, 126 et 108 ne sont pas premiers entre eux, ce qui te conduit à la réponse de Black Jack.
non, tu obtiens y=-18p-8 avec p dans Z, le premier k et le second k ne sont pas forcément les mêmes
ensuite tu ré-écris l'équation de départ.
tu tombes sur un truc du genre 126(k-p)=108, 126 et 108 ne sont pas premiers entre eux, ce qui te conduit à la réponse de Black Jack.
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
