Probléme sur propriété de cours

[LLG]

Bonjour à tous, j'ai vu dans mon cours qu'un endomorphisme de (E,N) (espace vectoriel normé de dimension quelconque) est continu si et seulement si il est lipschitzien...Mais je n'arrive pas à le demontrer...Pourriez vous m'aider...
D'avance MERCI.

[jose_latino]

Ce n'est pas difficile à démontrer que si une application linéaire est continue sur le 0, alors il est continue. Donc, Il faut que tu démontres que pour :
est continue sur 0 si et seulement s'il existe une constante 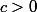telle que , pour tout .
C'est pas difficile montrer que cette dernière propriété est justement la condition d'être de Lipschitz. Clairement, être de Lipschitz implique continuité,

[abcd22]

C'est pourtant dans la réponse que je t'ai donnée à une question que tu as posée ici hier.