Propriété sur les paraboles

[Edward]

Bonjour,

Voilà l'énoncé :
Soit C une parabole, F son foyer, delta son axe focal, M € C. Montrer que la tangente en M à C (en bleu sur le dessin) est la bissectrice extérieures des droites (MF) et delta[m] (en rouge sur le dessin), cette dernière étant la parallèle à delta menée par M.



Je suis parti sur une méthode bourrin : on prend un point M sur la tangente, et on montre que les distances aux 2 droites sont égales. Mais les calculs deviennent vraiment monstrueux...

Je me demandais si quelqu'un avait une méthode plus simple pour ce problème, car j'ai beau réfléchir je n'en trouve pas d'autre...

Merci d'avance

[abcd22]

Bonsoir,
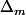
Pour prouver le résultat il suffit de prouver que F (ou n'importe quel point de MF mais puisqu'on a F sous la main...) a pour symétrique par rapport à la tangente un point de . Ça fait encore un peu de calculs mais beaucoup moins que ce que tu as essayé.

[Edward]

Merci pour l'idée abcd22, je tente ça de suite^^.

[abcd22]

Pour faire un peu moins de calculs ça doit être un peu plus rapide d'appeler H la projection de M sur la droite directrice de la parabole, de calculer le milieu du segment [HF] et de montrer qu'il est sur la tangente ; puisqu'on sait déjà que HM = HF c'est suffisant pour dire que H est le symétrique de F par rapport à la tangente.

[Edward]

là j'ai du mal à suivre... qu'appelle-tu directrice de la parabole ?

sinon pour moi ça marche bien , en plus à la question d'avant on avait prouvé que le projeté de F sur la tangente appartenait à (Oy) donc après ça tombe tout seul.

[abcd22]

Il y a plusieurs définitions possibles de la parabole, dont « l'ensemble des points M à égale distance d'une droite (la directrice) et d'un point (le foyer) n'appartenant pas à la droite » (donc avec les notations de mon message précédent ça donne tout de suite MH = MF).
Bon si vous n'avez pas parlé de ça et d'après la question d'avant, je suppose que ce n'était pas cette méthode qui était attendue.