Les suites

[Ahoud]

Bonsoir, je rencontre actuellement un petit problème pour cet exercice:

La suite (Un) est définie par U0=1 et pour tout entier naturel n supérieur ou égal à 1 :
Un= ((n*(Un-1))/ ( n+1)
( le -1 est sur le n or le +1 est après le n)
En admettant que tous les termes de la suite sont strictement positifs, étudier les variations de la suite.

Voilà où j'en suis :
( Un+1)-Un= ((n+1)*(Un+1-1))/ (n+1+1) - ((n*(Un-1)) / (n+1)
= ((n+1)*Un) / n+2 - (( n*(Un-1)) / (n+1))
Après cela, je suis un peu perdu, dois-je remplacer les Un restants par ce que est donné dans l'énoncé ?
Merci

[zaal]

Bonsoir !

Un+1 = (n+1)(Un) / (n+2)
Tu retrouves Un dedans.
Donc pas besoin de le remplacer dans ta formule Un+1 - Un, tu as juste besoin de remplacer Un+1 pour le moment.
Commence déjà par là pour voir si ça peut te débloquer

[Ahoud]

Merci pour la réponse.

Je dois donc remplacer (Un+1)(Un) / (n+2) mais par quoi ? Je n'ai pas d'autres indications, hormis Un

[zaal]

Alors aussi j'ai oublier de dire, ça me revient.
Lorsqu'une suite est strictement positive, il faut utiliser le rapport Un+1 / Un. Mais ce doit être dans ton cours non ?
De la, tu remplaces Un+1 par (n+1)(Un) / (n + 2) comme dis précédemment. Dis moi ce que tu trouves en faisant comme ça

[danyL]

Bonsoir, je rencontre actuellement un petit problème pour cet exercice:

La suite (Un) est définie par U0=1 et pour tout entier naturel n supérieur ou égal à 1 :
Un= ((n*(Un-1))/ ( n+1)
( le -1 est sur le n or le +1 est après le n)
En admettant que tous les termes de la suite sont strictement positifs, étudier les variations de la suite.

Voilà où j'en suis :
( Un+1)-Un= ((n+1)*(Un+1-1))/ (n+1+1) - ((n*(Un-1)) / (n+1)
= ((n+1)*Un) / n+2 - (( n*(Un-1)) / (n+1))
Après cela, je suis un peu perdu, dois-je remplacer les Un restants par ce que est donné dans l'énoncé ?
Merci

bonsoir
la relation est Un en fonction de Un-1
et pour étudier les variations tu calcules Un+1 - Un
du coup tu te retrouves avec 3 indices : Un+1, Un et Un-1

soit tu gardes la relation Un en fonction de Un-1
et tu calcules Un - Un-1

soit tu modifies les indices de la relation pour avoir Un+1 en fonction de Un
et là tu peux calculer Un+1 - Un

[zaal]

Salut danyL,
il me semble pourtant que la variation d'une suite strictement positive se déduit en faisant le rapport Un+1 / Un.

[Ben314]

Salut,
Personnellement, (et comme d'habitude...) pour étudier la monotonie d'une suite, je ne commence jamais par écrire sans réfléchir ni .
Je commence par réfléchir et regarder à quoi conduit l'inégalité qui est la définition de la croissance d'une suite, à savoir et/ou .
Ensuite (et uniquement ensuite), je me pose la question de savoir si j'ai intérêt à écrire l'inégalité plutôt sous la forme ou bien sous la forme (si 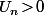) ou bien... sous une autre forme qui ne soit ni l'une ni l'autre.
Et bien évidement, le plus malin, ben... ça dépend du "contexte", c'est à dire de la suite donnée.

Bref, comme d'habitude, ben il faut réfléchir avant d'agir...

[zaal]

Ahoud ,

En faisant le remplacement U(n+1) par (n+1)(Un) / (n+2) dans la division U(n+1)/U(n) , tu arrives à

U(n+1)/U(n) = [ (n+1)(Un) / (n+2) ] / Un

= [ (n+1)(Un) / ( n + 2 ) ] * [ 1 / Un ]

Je ne vais pas plus loin. Mais développes ça et dis moi ce que tu trouves
Si tu as des questions de compréhension n'hésites pas

[zaal]

Salut,
Personnellement, (et comme d'habitude...) pour étudier la monotonie d'une suite, je ne commence jamais par écrire sans réfléchir ni .
Je commence par réfléchir et regarder à quoi conduit l'inégalité qui est la définition de la croissance d'une suite, à savoir et/ou .
Ensuite (et uniquement ensuite), je me pose la question de savoir si j'ai intérêt à écrire l'inégalité plutôt sous la forme ou bien sous la forme (si ) ou bien... sous une autre forme qui ne soit ni l'une ni l'autre.
Et bien évidement, le plus malin, ben... ça dépend du "contexte", c'est à dire de la suite donnée.

Bref, comme d'habitude, ben il faut réfléchir avant d'agir...

Tu as bien raison, ne jamais foncer tête baissée !
Mais là on sait d'après l'énoncé que c'est une suite strictement positive, la question ne se pose pas et donc l'utilisation du rapport U(n+1) / U(n) est évident.

[Ahoud]

Dans mon cours, on me dit d'utiliser ce rapport surtout en présence de puissance.
Du coup j'obtiens :
(n+1) / ( n+2) en ayant simplifier avec Un

[zaal]

Super c'est bien ça

[zaal]

Donc n'oublies pas, quand on te dit que la suite est strictement positive, utilise le rapport, ça doit être un réflexe pour tes exercices avenir

[Ahoud]

J'ai donc Un+1 < Un
Donc (Un) est décroissante

[zaal]

Regardes cette explication
https://www.cap-concours.fr/administrat ... e-s_mat_39

[Ben314]

Tu as bien raison, ne jamais foncer tête baissée !
Mais là on sait d'après l'énoncé que c'est une suite strictement positive, la question ne se pose pas et donc l'utilisation du rapport U(n+1) / U(n) est évident.

Ben... non...
C'est pas parce que B est strictement positif que tu as forcément intérêt à écrire que A>B équivaut à A/B>1.

Par exemple, si qui est bien strictement positif, pour montrer que la suite est croissante, ben ça me parait pas malin du tout d'écrire
Tu écrit quoi ensuite ?

[zaal]

Tu as bien raison, ne jamais foncer tête baissée !
Mais là on sait d'après l'énoncé que c'est une suite strictement positive, la question ne se pose pas et donc l'utilisation du rapport U(n+1) / U(n) est évident.

Ben... non...
C'est pas parce que B est strictement positif que tu as forcément intérêt à écrire que A>B équivaut à A/B>1.

Par exemple, si qui est bien strictement positif, pour montrer que la suite est croissante, ben ça me parait pas malin du tout d'écrire
Tu écrit quoi ensuite ?

Dans le cas que tu dis, u(n) est définit de manière explicite il suffit juste de faire une étude de sens de variation sur [0 ; +infini[ comme on le ferai pour une fonction.

[Ahoud]

https://www.cap-concours.fr/administrat ... e-s_mat_39
nous sommes dans le cas contraire ici ?

[zaal]

https://www.cap-concours.fr/administratif/preparation-aux-epreuves/mise-a-niveau-et-entrainement/determiner-le-sens-de-variations-d-une-suite-s_mat_39
nous sommes dans le cas contraire ici ?

Yes, car n+1 < n+2 donc (n+1)/(n+2) < 1

Si tu es intéressé, voici un petit pdf d'exemples sur lequel tu peux t'entrainer pour avoir les bases qu'il faut sur l'étude du sens de variation d'une suite.
http://gerard.tisseau.free.fr/Documents ... Suites.pdf

[zaal]

Pour vérifier aussi tes résultats lorsque tu as des doutes, n'hésites pas à utiliser la calculatrice en te mettant en mode suite. Ça te permettra de savoir où aller lorsque tu bloques également.
(Je dis bien que lorsque tu as des doutes ou pour vérifier ! L'utilisation de sa matière grise y a que ça de vrai pour bien s'entraîner )

[Ahoud]

Merci beaucoup