Résoudre un polynome de 4ème degré

[Akrone]

Bonjour,
Je suis bloqué sur la résolution du polynome de 4ème degré :


En effet, on demande de diviser l'équation par x², ce qui fait


puis de démontrer que ce qui est prouvé par l'identité

et d'en déduire que ça se ramenne à une équation de second degré d'inconue ce qui fait


Mais c'est quand il faut résoudre dans que je bloque..

Merci de votre aide !

[Tiruxa47]

Bonjour

Il ne doit pas y avoir à la fois des x et des u dans la même équation
On a
10(x²+1/x²) -77(x+1/x)+150=0

Ensuite effectue le changement

[Lostounet]

puis de démontrer que ce qui est prouvé par l'identité

Euh..Je ne connais pas cette identité je ne l'ai jamais vue. Tu es sûr?

[Akrone]

puis de démontrer que ce qui est prouvé par l'identité

Euh..Je ne connais pas cette identité je ne l'ai jamais vue. Tu es sûr?

Désolé, c'est corrigé

[Akrone]

Bonjour

Il ne doit pas y avoir à la fois des x et des u dans la même équation
On a
10(x²+1/x²) -77(x+1/x)+150=0

Ensuite effectue le changement

Merci, mais je ne vous pas trop comment on arrive a ce resultat

[Lostounet]

Salut,
Reprenons dès le début.

Tu veux résoudre l'équation de degré 4:


Ensuite, on te conseille de diviser l'équation par . On vérifie d'abord que x = 0 n'est pas une solution de l'équation déjà (en remplaçant x par 0, on trouve 10 = 0 ce qui n'est pas vrai). Donc on a le droit de diviser par x^2.

On trouve donc:


C'est maintenant que l'astuce va jouer son rôle: on va regrouper intelligemment les termes de la dernière équation comme suit:
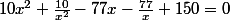
(j'ai rien fait.. j'ai juste changé l'ordre des termes de la somme).

Maintenant on constate que
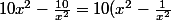Et que

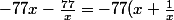Cela signifie que l'équation devient:


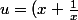Maintenant, à quoi toute cela sert? Tu vas voir. On va maintenant faire ce qu'on appelle un changement d'inconnue. On va poser et essayer d'écrire l'équation uniquement en utilisant "u" (sans faire intervenir 'x').
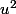
Ma question pour toi: que vaut ? Peux-tu écrire l'équation en utilisant uniquement u et u^2 ?

[Akrone]

Ah oui merci, c'est malin je l'avais pas vus !

vaudrait

donc on peux faire ce qui se ramenne à un polynome de second degré !

Merci !

[Lostounet]

Attention, u^2 ne vaut pas x^2+1/x^2 seulement...Tu as oublié quelque chose.

u^2=(x+1/x)^2=...utilise(a+b)^2.. (la question d'avant je veux dire).

(attention tu as fait deux fois la même erreur)

Donc x^2+1/x^2 = u^2 - 2 non?

[Akrone]

Roh oui désolé ^^ !

Ducoup on peux dire que ça nous donne serait égal à ?

[Lostounet]

C'est presque ça sauf que tu dois multiplier x^2 + 1/x^2 tout entier par 10 ! et comme u^2 - 2 = x^2 + 1/x^2
10(u^2 - 2) = 10(x^2 + 1/x^2)

Donc...?

Euh... je suis désolé mais je pense m'être trompé (c'est une toute petite erreur) ! J'ai mis un "-" à la place d'un "+" .. désolé ! (Je vais faire semblant que c'est pour voir si tu suivais)
Ici:

(j'ai rien fait.. j'ai juste changé l'ordre des termes de la somme).

Maintenant on constate que
Et que

Ben on constate que certes, mais y'a pas ça dans l'équation. Il y a


Donc en prenant , on s'est mis d'accord que c'est pas pareil que 10u^2 - 2...

[Akrone]

Hum oui..

Mais du coup ça donne est egal à

Mais quand je calcul les racines à partir du discriminant, elle ne résolvent pas l'équation

[Lostounet]

Que trouves-tu pour u ?

N'oublie pas que nous on s'en fout de l'équation 10u^2 - 77u + 130 = 0 . Ce qui compte c'est le "x" de l'équation du début !
Et n'oublie pas que, dans un passé lointain, on avait pris u = x + 1/x ! Et que tu dois trouver x en utilisant les valeurs de u que tu as trouvées now.

[Akrone]

Pour u j'ai trouvé 2.5 et 5.2 mais il vas falloir que je trouve une maniere d'extraire x de u = x + (1/x) !

Comme je suis pas futé je vais switcher sur un corpus sinon je surchaffe ! x)

Merci beaucoup !

[Lostounet]

Euh mais tu as presque fini!

Si u=2.5
2.5=x +1/x

Que se passe-t-il si on multiplie les deux côtés par x?

Tu dois faire un commentaire composé? ou dissertation?

[Akrone]

Ahah oui, mais si je continue, je suis contre productif x)

Ducoup ça me fait 2.5 = x + 1/x
= 2.5x = x + 1
= 1.5x = 1
= x = 1/1.5 = 0.6
et pour 5.2 j'ai 1/4.2 = 0.23

Ce qui est proche des deux racines 0.2 et 0.5 est-ce correcte ? ou j'ai encore fait des erreures ?

Merci !
PS: C'est plus un commentaire composé ^^

[Lostounet]

Ahah oui, mais si je continue, je suis contre productif x)

Ducoup ça me fait 2.5 = x + 1/x
= 2.5x = x + 1
= 1.5x = 1
= x = 1/1.5 = 0.6
et pour 5.2 j'ai 1/4.2 = 0.23

Ce qui est proche des deux racines 0.2 et 0.5 est-ce correcte ? ou j'ai encore fait des erreures ?

Merci !
PS: C'est plus un commentaire composé ^^

Euhh quand tu multiplies par x les deux côtés cela fait:
2.5x= x(x+1/x)

donc 2.5x= x^2 + 1 ! on distribue le x.

Tu croyais que la vie était belle et facile? C'est une autre équation du second degré qui t'attend !!! :p