Inéquation d'un polynôme du 4eme degré
18 messages
- Page 1 sur 1
Inéquation d'un polynôme du 4eme degré
Bonjour à tous,
J'essaie de résoudre cette inéquation : x^4-5x^2+3 ≥ 0.
J'ai d'abord essayer de mettre x^2 en facteur mais ce qui me gène c'est le 3, du coup je suis bloqué.
Quelqu'un pourrai me mettre sur la piste svp, j'ai pensé à la méthode d'Horner mais j'arrive pas à l'utiliser ici.
Merci d'avance !!
J'essaie de résoudre cette inéquation : x^4-5x^2+3 ≥ 0.
J'ai d'abord essayer de mettre x^2 en facteur mais ce qui me gène c'est le 3, du coup je suis bloqué.
Quelqu'un pourrai me mettre sur la piste svp, j'ai pensé à la méthode d'Horner mais j'arrive pas à l'utiliser ici.
Merci d'avance !!
Re: Inéquation d'un polynôme du 4eme degré
C'est une équation bicarrée, du second degré en 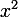 . Poser
. Poser  , et commencer par résoudre en
, et commencer par résoudre en 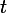 .
.
Re: Inéquation d'un polynôme du 4eme degré
Salut,
Tu n'arriveras pas à mettre x^2 en facteur vu qu'il n'est pas en commun avec les trois termes.
Par contre tu peux essayer de poser y=x^2 et exprimer ton polynôme avec y seulement.
Cela devient une simple inéquation de degré 2 d'inconnue y ... Commence par factoriser ce polynôme.
Tu n'arriveras pas à mettre x^2 en facteur vu qu'il n'est pas en commun avec les trois termes.
Par contre tu peux essayer de poser y=x^2 et exprimer ton polynôme avec y seulement.
Cela devient une simple inéquation de degré 2 d'inconnue y ... Commence par factoriser ce polynôme.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Inéquation d'un polynôme du 4eme degré
Ah ok j'en avais jamais entendu parler... Merci à vous !!
Donc si je comprends bien, si on pose T=x2 l'équation devient T^2-5T+3 ≥0.
Je trouve deux solutions: x1 = 5+racine(13) / 2 et x2= 5-racine(13) / 2.
Je fais le tableau de signe et je trouve que la fonction est positive sur (moins l'infinie, 5-racine(13) / 2 et +racine(13) / 2, plus l'infinie) et négative entre les deux racines.
Mais du coup, la fonction polynôme de départ (en degré 4) aura les mêmes racines que la fonction T^2-5T+3 ≥0 ??
Merci à vous ! !
Donc si je comprends bien, si on pose T=x2 l'équation devient T^2-5T+3 ≥0.
Je trouve deux solutions: x1 = 5+racine(13) / 2 et x2= 5-racine(13) / 2.
Je fais le tableau de signe et je trouve que la fonction est positive sur (moins l'infinie, 5-racine(13) / 2 et +racine(13) / 2, plus l'infinie) et négative entre les deux racines.
Mais du coup, la fonction polynôme de départ (en degré 4) aura les mêmes racines que la fonction T^2-5T+3 ≥0 ??
Merci à vous ! !
Re: Inéquation d'un polynôme du 4eme degré
vladi a écrit:...et quand ce sera traité
tu termine en traitant
Oui mais on a pris T=x2 donc faire x^2-T = 0 revient à faire x^2 - x^2 = 0 ?? Je suis un peu perdu désolé
Re: Inéquation d'un polynôme du 4eme degré
il faut que pour chaque T vérifiant l'inégalité(ça tu sais le faire c'est ton cours de seconde) tu prenne ce T
et que tu solve (et ça aussi tu sais le faire c'est ton cours de seconde)
(et ça aussi tu sais le faire c'est ton cours de seconde)
bon courage cher camarade
et que tu solve
bon courage cher camarade
Re: Inéquation d'un polynôme du 4eme degré
Ah d'accord, tu veux dire que pour chacune des racines de T^2-5T+3 = 0 soit
* T1= 5+racine(13) / 2 et
* T2 x2= 5-racine(13) / 2, je dois de nouveau résoudre x2 - T1 = 0 et x2 - T2 = 0.
Okok je vois pas bien pourquoi on fais ça mais je vais faire ça merci !!
* T1= 5+racine(13) / 2 et
* T2 x2= 5-racine(13) / 2, je dois de nouveau résoudre x2 - T1 = 0 et x2 - T2 = 0.
Okok je vois pas bien pourquoi on fais ça mais je vais faire ça merci !!
Re: Inéquation d'un polynôme du 4eme degré
Legolas2mars a écrit:Ah d'accord, tu veux dire que pour chacune des racines de T^2-5T+3 = 0
non non non camarade
rappelle toi on recherche d'abord les T qui vérifient l'inégalité (et là toi tu as écrit une égalité)
Re: Inéquation d'un polynôme du 4eme degré
Arrghrr l'inégalité T^2-5T+3 ≥0 je l'ai déjà résolue plus haut et j'ai trouvé T1= 5+racine(13) / 2 et T2= 5-racine(13) / 2 mais ça c'est pour l'équation T^2-5T+3 ≥0 et non x^4-5x^2+3 ≥ 0. Je ne comprends pas comment on rebascule à cette premiere équation.... en faisant x2 - T1 = 0 et x2 - T2 = 0 ??? Pas sûr... Je suis largué...
Re: Inéquation d'un polynôme du 4eme degré
rappelez vous du signe du trinôme qui va vous donner les bonnes valeurs de T qui vérifient l'inégalité
il faut que vous réfléchissiez à froid (prenez l'exemple sur Osterman dans le film Osterman Week-end de Sam Peckinpah : il s'en sort à la fin car c'est un serpent)
il faut que vous réfléchissiez à froid (prenez l'exemple sur Osterman dans le film Osterman Week-end de Sam Peckinpah : il s'en sort à la fin car c'est un serpent)
Re: Inéquation d'un polynôme du 4eme degré
Legolas2mars a écrit:Ah d'accord, tu veux dire que pour chacune des racines de T^2-5T+3 = 0 soit
* T1= 5+racine(13) / 2 et
* T2 x2= 5-racine(13) / 2, je dois de nouveau résoudre x2 - T1 = 0 et x2 - T2 = 0.
Okok je vois pas bien pourquoi on fais ça mais je vais faire ça merci !!
Resalut,
Tu es largué car tu as oublié ce qu'on cherche.
On n'est pas en train de résoudre x^4-5x^2+3=0 mais de trouver les x tels que x^4-5x^2+3>=0
Ce n'est pas la même chose...Nous devons faire un tableau de signes pour résoudre cette inéquation.
Ce que tu as commencé par faire c'est poser T=x^2.
Ensuite tu as démontré que quel que soit le réel T,
T^2-5T+3 = (T - (5+sqrt(13))/2)(T-(5 - sqrt(13))/2
Cela veut dire que, comme T=x^2:
x^4-5x^2+3 = (x^2 - (5+sqrt(13))/2)(x^2-(5-sqrt(13))/2)
Il faut maintenant regarder le signe de chacun des facteurs à droite pour voir quand est-ce que leur produit est positif, pour quels x a-t-on:
x^2-(5+sqrt(13))/2 positif? Négatif?
Même question pour l'autre...
Il faut donc faire un tableau de signe mettant en jeu les deux termes du produit et étudier les signes des deux puis le signe de leur produit.
PS: je n'ai pas vérifié les calculs menés mais c'est l'idée.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Inéquation d'un polynôme du 4eme degré
En fait, faut utiliser la forme factorisée à partir des racines !!! Merci les gars c'est ce qu'il me manquait !! 

Re: Inéquation d'un polynôme du 4eme degré
Normalement tu connais le signe d'un trinôme en fonction de la position relative par rapport aux racines, et au signe de a ( parabole en "sourire" ou en "sourire inversé")
Re: Inéquation d'un polynôme du 4eme degré
Bonjour ;
Voici un autre chemin qui utilise la forme canonique et une identité remarquable .
^2 - \dfrac{13}{4} = (x^2 - \dfrac{5}{2})^2 - (\dfrac{\sqrt{13}}{2})^2)
(x^2 - \dfrac{5 - \sqrt{13}}{2}) = (x^2 - \sqrt{\dfrac{5 + \sqrt{13}}{2}}^2)(x^2 - \sqrt{\dfrac{5 - \sqrt{13}}{2}}^2))
(x + \sqrt{\dfrac{5 + \sqrt{13}}{2}})(x - \sqrt{\dfrac{5 - \sqrt{13}}{2}})(x^2 + \sqrt{\dfrac{5 - \sqrt{13}}{2}})) .
.
Il suffit maintenant - comme l'a dit Lostounet - de conclure avec un tableau de signes , qui plus ici est un tableau de signes d'un produit de quatre facteurs de premier degré .
Voici un autre chemin qui utilise la forme canonique et une identité remarquable .
Il suffit maintenant - comme l'a dit Lostounet - de conclure avec un tableau de signes , qui plus ici est un tableau de signes d'un produit de quatre facteurs de premier degré .
18 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
