Bonjour, j'ai un devoir maison de maths spé mais je butte sur une équation et je viens vers vous pour peut être récolté une réponse .
L'énoncé est le suivant :
Résoudre dans N3( au cube):
xyz=4(x+y+z)
En vous remerciant d'avance , Paul.
Dm de maths spé
5 messages
- Page 1 sur 1
Re: Dm de maths spé
Salut,
Supposons que x<=y <= z.
Alors x+y+z<= 3z donc 4(x+y+z)<=12z
Or xyz=4(x+y+z)
Donc xyz <=12z
Ce qui signifie que xyz <= 12z et que donc, si z est non nul, xy<12
Quels sont les entiers dont le produit est inférieur à 12? avec x<=y
Ce sont x=3, y= 4
x=1, y = 12
x=2, y= 3
x=2, y=4
...
Bon il y en a quelques uns.
Ensuite tu regardes si la valeur de z qu'on trouve est entière.
Exemple: x=2 et y=4
xyz=4(x+y+z)
8z= 24+4z
z=...
Supposons que x<=y <= z.
Alors x+y+z<= 3z donc 4(x+y+z)<=12z
Or xyz=4(x+y+z)
Donc xyz <=12z
Ce qui signifie que xyz <= 12z et que donc, si z est non nul, xy<12
Quels sont les entiers dont le produit est inférieur à 12? avec x<=y
Ce sont x=3, y= 4
x=1, y = 12
x=2, y= 3
x=2, y=4
...
Bon il y en a quelques uns.
Ensuite tu regardes si la valeur de z qu'on trouve est entière.
Exemple: x=2 et y=4
xyz=4(x+y+z)
8z= 24+4z
z=...
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Dm de maths spé
d'accord je vois , j'avais vu un corrigé de ce type sur internet mais j'hésitais, je ne savais pas s'il fallait supposer 0<x<y<z ou essayer de résoudre comme cela .
Merci beaucoup
Merci beaucoup
Re: Dm de maths spé
En fait c'est l'astuce classique.
Mais on peut le supposer car c'est pareil de supposer y<=x<= z ou autre. Une fois tu trouves (x;y;z) qui marchent tu peux remarquer que (z;x;y) marche aussi (il te suffit de recopier ...)
Mais on peut le supposer car c'est pareil de supposer y<=x<= z ou autre. Une fois tu trouves (x;y;z) qui marchent tu peux remarquer que (z;x;y) marche aussi (il te suffit de recopier ...)
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Dm de maths spé
Salut,
Perso, vu la tête du truc, j'essayerais bien de copier la méthode classique concernant les équation du type xy=3x+5y+7 qu'on écrit xy-3x-5y=7 puis où on dit que xy-3x-5y, c'est "presque" (x-5)(y-3) sauf qu'il manque le +15 à la fin donc l'équation équivaut à xy-3x-5y+15=7+15 c'est à dire (x-5)(y-3)=22 et y'a plus qu'a chercher les factorisation possible de 22.
Sauf que là, il y a du xyz avec le z qui fait c..., mais on peut faire comme si c'était un paramètre pour voir ce que ça donne. Comme pour avoir du xy=... faut diviser par z, on commence par regarder le cas particulier z=0 qui donne clairement l'unique solution x=0 ; y=0 (car les entiers doivent être positifs; dans Z il y aurait d'autres solutions).
Pour z non nul on a alors :
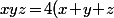\ \Leftrightarrow\ <br />xy\!-\!\dfrac{4}{z}x\!-\dfrac{4}{z}y\!=\!4\ \Leftrightarrow\ <br />\Big(x\!-\!\dfrac{4}{z}\Big)\Big(y\!-\dfrac{4}{z}\Big)\!=\!4\!+\!\dfrac{16}{z^2}\ \Leftrightarrow\ <br />(zx\!-\!4)(zy\!-\!4)\!=\!4z^2\!+\!16)
qui permet facilement de trouver les solutions pour un fixé (il suffit de chercher les factorisations de
fixé (il suffit de chercher les factorisations de  )
)
Or, une fois trouvé "à la main" les solutions pour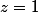 ,
, 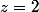 ,
, 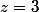 , c'est fini vu que, par symétrie de l'énoncé, on connait en fait toutes les solutions où une des trois variables est
, c'est fini vu que, par symétrie de l'énoncé, on connait en fait toutes les solutions où une des trois variables est 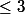 or, si elles étaient toutes les trois
or, si elles étaient toutes les trois  , on aurait
, on aurait
(zy\!-\!4)\!\geq\!(4z\!-\!4)^2\!=\!16z^2\!-\!32z\!+\!16\!=\!4z^2\!+\!16\!+\!4z(3z\!-\!8)>4z^2\!+\!16)
Perso, vu la tête du truc, j'essayerais bien de copier la méthode classique concernant les équation du type xy=3x+5y+7 qu'on écrit xy-3x-5y=7 puis où on dit que xy-3x-5y, c'est "presque" (x-5)(y-3) sauf qu'il manque le +15 à la fin donc l'équation équivaut à xy-3x-5y+15=7+15 c'est à dire (x-5)(y-3)=22 et y'a plus qu'a chercher les factorisation possible de 22.
Sauf que là, il y a du xyz avec le z qui fait c..., mais on peut faire comme si c'était un paramètre pour voir ce que ça donne. Comme pour avoir du xy=... faut diviser par z, on commence par regarder le cas particulier z=0 qui donne clairement l'unique solution x=0 ; y=0 (car les entiers doivent être positifs; dans Z il y aurait d'autres solutions).
Pour z non nul on a alors :
qui permet facilement de trouver les solutions pour un
Or, une fois trouvé "à la main" les solutions pour
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
