Divisibilité

[teter]

Bonjour j'ai juste une petite question:
est ce que "6 divise (7^n)+1" signifie "(7^n)+1= 6xq" ?

[chan79]

salut
oui, 6 divise s'il existe un nombre entier tel que

A noter que est toujours divisible par 6 mais 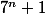ne l'est jamais.

[teter]

D'accord mais c'est normal que pour n'importe quelle valeur n je trouve k qui sont toujours des fractions ?

[chan79]

comme je l'ai mis juste au dessus, n'est jamais divisible par 6 (quelle que soit la valeur de n)

[teter]

Dans le DM on me dit qu'elle n'est pas vraie pour tout entier naturel n supérieur ou égal à zéro, mais qu'elle est héréditaire, pourquoi ?

[beagle]

Dans le DM on me dit qu'elle n'est pas vraie pour tout entier naturel n supérieur ou égal à zéro, mais qu'elle est héréditaire, pourquoi ?

héréditaire dit justement que si c'était vrai pour n, alors cela serait vrai pour n+1

d'où l'intérèt de l'initialisation fausse!!!!
ouh heureusement les gars c'est même pas vrai depuis le début!

[chan79]

Tu supposes:
tu considères

Remplaces par

[zygomatique]

salut

dire qu'une propriété fausse P(n) est héréditaire c'est simplement dire : F => F est vrai

et c'est une tautologie de dire que F => F est vrai (pour celui qui connait la logique)

bien entendu il reste l'exercice intéressant de montrer que c'est effectivement vrai ...

[beagle]

Bof, l'hérédité qui fonctionne alors que l'initialisation n'est pas réalisée
est un phénomène bien plus intéressant que le F implique F

[zygomatique]

dans le cas présent on dit cependant la même chose ... mais il est évident qu'en logique on utilisera mon langage et en récurrence on utilisera le langage ... de la récurrence !! et donc le terme d'hérédité (qui n'est qu'une simple implication dont on cherche la véracité)

...

[beagle]

dans le cas présent on dit cependant la même chose ... mais il est évident qu'en logique on utilisera mon langage et en récurrence on utilisera le langage ... de la récurrence !! et donc le terme d'hérédité (qui n'est qu'une simple implication dont on cherche la véracité)

...

l'hérédité qui fonctionne est plus spécifique que le généraliste F implique F
et je trouve plus rigolo mais bon!

[teter]

Je dois expliquer pourquoi elle est héréditaire alors que la propriété n'est pas vraie pour tout entier supérieur ou égal à 0, je dois expliquer comment ?

[beagle]

Je dois expliquer pourquoi elle est héréditaire alors que la propriété n'est pas vraie pour tout entier supérieur ou égal à 0, je dois expliquer comment ?

Comme l'a dit Chan
tu supposes que c'est vrai pour n
tu examine avec n+1 ce qui se passe alors

[teter]

Dans la question précédente on devait montrer qu'elle était héréditaire et je l'ai fait mas j'arrive pas à expliquer avec des mots pourquoi elle est héréditaire alors qu'elle n'est pas vrai la propriété

[beagle]

Dans la question précédente on devait montrer qu'elle était héréditaire et je l'ai fait mas j'arrive pas à expliquer avec des mots pourquoi elle est héréditaire alors qu'elle n'est pas vrai la propriété

cela veut dire que tu ne comprends pas le role de l'initialisation dans la démonstration par récurrence.

L'hérédité dit juste si cela était vrai pour n, alors ce serait vrai pour n+1
si c'est vrai pour n alors c'est vrai pour n+1

Donc il faut voir grace à l'initialisation
c'est vrai pour 1, donc cela le sera pour 2 donc cela le sera pour 3 donc cla le sera pour 4.
Donc là tu as démontré que cela sera vrai tout le temps.

Mais parfois l'hérédité est vraie, si c'était vrai pour n alors cela serait vrai pour n+1
et là ben cela se termine en, mais ce n'est pas vrai pour 1
donc le si 1 est vrai alors j'aurais 2 n'existe pas puisque en 1 c'est faux.Donc de 1 faux on ne peut déduire que 2 est vrai, donc on ne peut déduire de 2 que 3 est vrai etc...

[beagle]

Encore un petit tour de manège.

A= l'expression en n
B= l'expression en n+1

Le si j'ai A alors j'ai B est aussi un
si j'avais A, alors j'aurais B
Lorsque A alors B
Quand j'aurais A alors j'aurais B

retour à la récurrence avec le
quand j'aurais A alors j'aurais B:

1)premier cas l'initialisation ne marchera pas, jamais
le quand j'aurais A devient: tu l'auras jamais mon pote!
oui mais je veux avoir B,
ben quand tu auras A mon fils,
mais papa t'as dit que j'aurais jamais A
Bon ben alors fais-toi une idée pour le B n'y compte pas, même à Noël.
Voilà ça c'est ton cas, c'est l'exo
si cela marche pour n, alors cela marchera pour n+1
oui mais voilà cela ne marche pas pour n.

2)second cas, l'initialisation marche, mais uniquement après ou pour n=5 (c'est une exemple, hein!)
quand j'aurais A alors j'aurais B
je n'ai pas A pour n= 0 à 4
j'ai A qui est vrai pour n=5,
et bien tu démontres alors par récurrence que pour tout entier supérieur à 4 ton expression en n est valable.
ce n'est pas le cas pour n=2 par exemple.


Marchait plutôt bien l'utilisation de l'implication du si A alors B
avec implicite quand A vrai
c'est quand j'ai A que...
le quand j'ai A j'ai B avec A faux, ben je m'en tape, t'as pas A quoi espèce de baratineur.

[chan79]

salut
Admettons qu'on ait positionné 1000 dominos de sorte que si l'un tombe, le suivant tombera.
Tant qu'on ne fera pas tomber le premier (initialisation), rien de se passera.

[beagle]

je vais enfoncer le même clou, donc ok je radote mais

l'idée de l'abandon du implique au lycée
l'idée de l'abandon du si A alors B au lycée (au profit d'un A donc B)

et bien cela empèche bien de comprendre que le si A ne dépend pas de A est vrai ou A est faux,
le si A est une hypothèse, si j'avais A, si A est vrai, alors que se passe-t-il...

c'est vrai de l'hérédité de la récurrence, c'est vrai du raisonnement par l'absurde,
dans ces deux cas le A est ou peut-être faux, mais on examine le A vrai
quand A alors ...

Versus un apprentissage avec A donc B
ben on ne comprend rien à l'utilisation du A faux

bref contrairement à ce que dit zygomatique, ce n'est pas parce que A faux implique B est vrai
c'est parce que si A était vrai alors j'aurais B.

Maintenant comme je suis le seul à partager ce truc,...

[zygomatique]

[beagle]

:?:

C'est un problème de langage mathématique:

1)le langage usuel actuel (enfin tel que je le comprends, je ne l'ai fort heureusement pas SUBI)
dans la récurrence on fait:
initialisation
puis
n donc n+1

2)Dans le temps où c'était mieux avant comme le disent toujours les vieux radoteurs (enfin tel que je l'ai vécu heureux)
initialisation
si n alors n+1

Quelle différence?
Si j'ai n alors j'ai n+1
se dit également
lorsque..., quand...et avec le verbe avoir à tous les temps
si j'avais, si j'ai, juste éviter le si j'aurais, on aura

lorsqu'on aura n alors on aura n+1

premier cas: on n'aura jamais n en initialisation,
ben c'est pas génant d'avoirdémontré que si n alors n+1,
vu qu'on n'aura jamais n bref ça marche pas

second cas: initialisation fonctionne à n=3
lorsque on aura n vrai, ben pas à 0, pas à 1, pas à 2,
on aura n vrai à pertir de 3
etc...



Bref un langage mathématique au service du raisonnement en utilisant le si A alors B,un langage mathématique pour les étudiants,

versus un langage mathématique rigoureux qui ne sert pas très bien le raisonnement, bref un langage mathématique post-étudiant, A donc B


Et à priori je dirais que c'est idem pour le raisonnement par l'absurde:
si les droites étaient parallèles alors somme des angles dans le triangle dépasse 180
du si A alors B
un SI hypothèse, hypothèse qui ne marche pas

l'absurde avec
les droites parallèles donc la somme des angles dans le triangle dépasse 180
oui, et alors?Tu veux dire que si on avait ça, alors...
Ben dis le moi!


Et tout ceci est idem lorsque zygomatique répond sur la définition d'évènements indépendants:
la formule p(A inter B) = p(A)p(B)
en rajoutant épicétou
on voit bien là des maths de la rigueur qui utilisent le langage de celui qui connaît les maths (postétudiant) et non pas les maths de la compréhension du sujet de celui qui apprend (étudiant)

CQFD!