Bon, ben.... je comprend toujours pas très bien....
Tu peut m'expliquer en quoi la formule que tu donne, à savoir (2n-3)(2n-4)(2n-5)...(2n-k) n'est pas "
une formule mathématique permettant d'obtenir le résultat directement" ?
Parce que, certes, on peut l'écrire en utilisant le symbole factorielle ce qui la rend plus concise (donc plus rapide à écrire ce qui est éventuellement le but du jeu), mais par contre, en terme de "rapidité de calcul", ça aurait plutôt tendance à rallonger (il me semble quand même que c'est plus rapide de calculer directement 6*5 que de calculer (6*5*4*3*2*1)/(4*3*2*1), non ?)
Bref, si tu avait un peu de temps pour expliquer ce que tu compte faire avec cette formule de façon à mieux cerner ce que tu veut dire par "
une formule mathématique permettant d'obtenir le résultat directement", je pense que ça pourrait être utile.
EDIT : En fait, si le but du jeu c'est d'avoir une formule la plus concise possible, en général, ce que fait le matheux de base, c'est d'écrire "Je pose
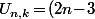(2n\!-\!4)...(2n\!-\!k))
", voire même
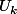
(ou

) si le

(ou le

) reste le même du début à la fin de la prose : on fait difficilement plus concis.


