Soit les points A(-2;-2), B(7;1) C(2;6)
1.a) Montrer qu'un point M du plan appartient à la médiatrice du segment si et seulement si MA^2=MB^2
b) Soit M un point de coordonné (x;y). Donner l'expression de MA^2 et de MB^2 en fonction de x et de y
c) En déduire qu'un équation de la médiatrice de [AB] est : y=-3x+7
2. Démontrer de même qu'un équation de la médiatrice de [BC] est : y=x-1
3. Soit R le centre du cercle circonscrit au triangle ABC.
a) Ecrire un système d'équation à deux inconnues de solution les coordonnées de R
b) Déterminer les coordonnées de R
Sujet DM seconde
4 messages
- Page 1 sur 1
Re: Sujet DM seconde
bonjour
"bonjour " et "merci" sont deux mots francais que l'on peut utiliser......, si!
pour que l'on puisse t'aider ( et non faire le travail a ta place) commence par nous dire ce que tu as fait et ou tu rencontre des difficultes........
les deux premieres questions sont des applications directes du cours...
.......
"bonjour " et "merci" sont deux mots francais que l'on peut utiliser......, si!
pour que l'on puisse t'aider ( et non faire le travail a ta place) commence par nous dire ce que tu as fait et ou tu rencontre des difficultes........
les deux premieres questions sont des applications directes du cours...
.......
Re: Sujet DM seconde
Bonjour ...
1/a/ "Montrer qu'un point M du plan appartient à la médiatrice du segment.." [AB] je suppose.
revient à la définition d'une médiatrice tu verra qu'un point qui appartient a la médiatrice d'un segment est situé a égale distance des deux points du segment. Il ne te reste plus qu'a traduire cela par des égalités
b/ Trouve les coordonnés de (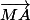 et ( \vec{MB}) )
)
et tu peux ensuite calculer MA et MB en utilisant la formule ;
Si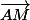 (x,y) alors AM=
(x,y) alors AM=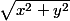
c/ Utilise les deux questions précédentes pour déterminer la relation qu'on te donne
2/ tu doit refaire exactement la même chose que toute la question 1 tu refait toutes les étapes .
1/a/ "Montrer qu'un point M du plan appartient à la médiatrice du segment.." [AB] je suppose.
revient à la définition d'une médiatrice tu verra qu'un point qui appartient a la médiatrice d'un segment est situé a égale distance des deux points du segment. Il ne te reste plus qu'a traduire cela par des égalités
b/ Trouve les coordonnés de (
et tu peux ensuite calculer MA et MB en utilisant la formule ;
Si
c/ Utilise les deux questions précédentes pour déterminer la relation qu'on te donne
2/ tu doit refaire exactement la même chose que toute la question 1 tu refait toutes les étapes .
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 66 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
