Intégrale trigonométrique
18 messages
- Page 1 sur 1
 Intégrale trigonométrique
Intégrale trigonométrique
Bonjour à tous !
Il m'a été donné pour Lundi un DM de math sauf que à vrai dire je n'y comprends pas grand chose. Donc si une âme charitable veut bien m'aider voici l'énoncé :
Il m'a été donné pour Lundi un DM de math sauf que à vrai dire je n'y comprends pas grand chose. Donc si une âme charitable veut bien m'aider voici l'énoncé :
- Fichiers joints
-
- 18643754_10207279059533758_644070672_n.jpg (58.13 Kio) Vu 684 fois
Re: Intégrale trigonométrique
Si a = b = 0, tu as une intégrale très facile pourtant...
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Intégrale trigonométrique
Pour moi ici, je trouve le résultat de 2pi mais je ne sais pas du tout si c'est ça 
Re: Intégrale trigonométrique
Ben oui tout simplement, c'est l'intégrale de 0 à 2 pi de cos(0)*cos(0) = 1*1 = 1
Pour le b), tu dois cherche une primitive de la fonction cos(ax)cos(bx) = cos(ax)*cos(ax) = cos(ax)^2.
Pour le b), tu dois cherche une primitive de la fonction cos(ax)cos(bx) = cos(ax)*cos(ax) = cos(ax)^2.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Intégrale trigonométrique
D'accord merci,
Donc si je comprends bien je le passe en puissance et après j'utilise la formule 1/2[1+cos(2ax)] ?
Et est-ce que je fais de même pour le b, par exemple 1/2[1+cos(2ax)] + 1/2[1+cos(2bx)] ?
Donc si je comprends bien je le passe en puissance et après j'utilise la formule 1/2[1+cos(2ax)] ?
Et est-ce que je fais de même pour le b, par exemple 1/2[1+cos(2ax)] + 1/2[1+cos(2bx)] ?
Re: Intégrale trigonométrique
Je ne comprends pas pourquoi tu veux faire de même pour b.
On a déjà utilisé l'hypothèse a = b en remplaçant le b par a pour trouver cos^2(ax) non?
De toute manière a=b, tu n'as donc pas besoin de distinguer a et b .. c'est le même nombre.
On a déjà utilisé l'hypothèse a = b en remplaçant le b par a pour trouver cos^2(ax) non?
De toute manière a=b, tu n'as donc pas besoin de distinguer a et b .. c'est le même nombre.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Intégrale trigonométrique
Ah oui d'accord je n'avais pas saisi que l'on utilisait l'hypothèse de a=b.
Du coup cela nous donnerait :
cos^2(alpha*x) = 1/2 [1+cos(2alpha*x)]
= 1/2 + 1/2cos(2alpha*x)
= 1/2 + cos(alpha*x)
= 1/2 + cos(alpha*(a+2pi)) - (1/2 + cos(alpha*a))
= cos (alpha*(a + 2pi)) - cos (alpha*a)
= cos (2pi)
= 1
Du coup cela nous donnerait :
cos^2(alpha*x) = 1/2 [1+cos(2alpha*x)]
= 1/2 + 1/2cos(2alpha*x)
= 1/2 + cos(alpha*x)
= 1/2 + cos(alpha*(a+2pi)) - (1/2 + cos(alpha*a))
= cos (alpha*(a + 2pi)) - cos (alpha*a)
= cos (2pi)
= 1
Re: Intégrale trigonométrique
Depuis quand cos(2ax)/2 donne cos(ax) ? 
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Intégrale trigonométrique
Ah mince je me disais bien que c'était trop beau pour être vrai.. du coup ça complique un petit peu les choses 
Re: Intégrale trigonométrique
Cela vous semble-t-il correcte ?
- Fichiers joints
-
- b.jpg (175.55 Kio) Vu 619 fois
Re: Intégrale trigonométrique
Salut, il y a une erreur de développement quand tu évalues en a+2pi à la fin, un alpha a disparu. Et du coup ta conclusion est foireuse si alpha n'est pas un entier.
Re: Intégrale trigonométrique
J'avoue que je ne retrouve pas le alpha qui a disparu, c'est à quelle ligne ?
Re: Intégrale trigonométrique
passage de 1/2 (2pi) + .... à la ligne suivante:: sin(2alpha(a+2pi) cela donne sin(2alpha a + 4alphapi)
Re: Intégrale trigonométrique
Parfait merci, j'ai réussi mais j'ai maintenant une intégrale plus complexe à résoudre où je ne sais pas comment faire pour les questions b) et c). C'est la même intégrale que toute à l'heure avec cos(alphax) * sin(betax).
Si vous pouviez me donner une piste pour que je commence au moins quelque chose. Merci beaucoup pour vos réponses !
Si vous pouviez me donner une piste pour que je commence au moins quelque chose. Merci beaucoup pour vos réponses !
Modifié en dernier par sarah2627 le 21 Mai 2017, 21:03, modifié 1 fois.
Re: Intégrale trigonométrique
C'est par rapport à l'exercice de départ? Tu viens de traiter le cas alpha = béta (b) , il te reste la question c), c'est cela?
Re: Intégrale trigonométrique
Toutes questions se traitent en linéarisant tes expressions ( apprends pour cela, les formules cos(a+b), cos(a-b), sin(a+b), sin(a-b) ou retrouve-les à l'aide des exp complexes)
Dans ton exo, i faut utiliser cos(alphax)sin(bétax) = [sin((béta+alpha)x) + sin((béta-alpha)x)]/2, que tu peux intégrer facilement quand alph diff de béta, le cas alpha =béta est facile.
Dans ton exo, i faut utiliser cos(alphax)sin(bétax) = [sin((béta+alpha)x) + sin((béta-alpha)x)]/2, que tu peux intégrer facilement quand alph diff de béta, le cas alpha =béta est facile.
Re: Intégrale trigonométrique
Bonjour ;
On a :
\cos(\beta x)=\frac{1}{2} (\cos((\alpha-\beta)x) + \cos((\alpha+\beta)x)),)
donc :
\cos(\beta x) dx=\frac{1}{2}\int_a^{a+2\pi} (\cos((\alpha-\beta)x) + \cos((\alpha+\beta)x))dx .)
Cela montre que les cas à étudier sont :
1) et
et 
2) ( ou
ou  ) et
) et 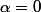 qui est équivalent à :
qui est équivalent à : 
3) ( ou
ou  ) et
) et 
On a :
donc :
Cela montre que les cas à étudier sont :
1)
2) (
3) (
18 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
