Maths 1L

[Kabyle]

Bonjour,
J'ai un DM de maths pour après les vacances seulement je suis bloquée sur une question ce qui fait que je ne peut pas répondre à toutes les suivantes...

Soit f la fonction définie sur I=[0.5;4] par f(x)=6x+8+

a)Déterminer la fonction dérivée de f (J'ai trouvé 6-(24/x²)
b)Montrer que la dérivée de f peut s'écrire f'(x)= sur I

Je bloque donc sur la question b, ne sachant absolument pas comment faire je fais appel à vous, je ne demande en aucun cas les réponses mais de l'aide, merci à ceux qui prendront leurs temps pour m'aider.

[laetidom]

Bonjour,

Si f est tout sur un même dénominateur, , au numérateur mettre en facteur par 6 puis on tombe sur a² - b² = . . .

[capitaine nuggets]

Salut !

a) Que trouves-tu ?
b) Développe l'expression de f' donnée dans la question. Si tu trouves la même expression que dans a) (après ça dépend peut-être de la forme du résultat que tu as donné lors de cette question) alors c'est bon.

[WillyCagnes]

bjr
f(x)=6x+8+24/x
la derivée de chaque terme
(6x)'=6
(8)'=0
(24/x)'=-24/x²

f'(x)=tu fais la somme et ensuite tu mets 6 en facteur (a²-b²)/x²

[pascal16]

petit rappel car en 1L, les mises sous même dénominateur ne sont pas encore faites sur le bout des doigts, un exemple :

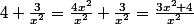
[Kabyle]

Salut !

a) Que trouves-tu ?
b) Développe l'expression de f' donnée dans la question. Si tu trouves la même expression que dans a) (après ça dépend peut-être de la forme du résultat que tu as donné lors de cette question) alors c'est bon.

En a j'ai trouvé 6-(24/x²)

[Kabyle]

Bonjour,

Si f est tout sur un même dénominateur, , au numérateur mettre en facteur par 6 puis on tombe sur a² - b² = . . .

f n'est pas tout sur le meme dénominateur, c'est f'

[laetidom]

f n'est pas tout sur le meme dénominateur, c'est f'

Oui, mais si c'est justement la forme que tu as trouvé qui te gêne,

si on dit que alors

est-ce plus facile maintenant pour obtenir la forme demandée ? . . .

[Kabyle]

C'est ce que je viens de faire mais là je suis en train de factoriser avec 6 en facteur mais je suis bloquée à

[laetidom]

C'est ce que je viens de faire mais là je suis en train de factoriser avec 6 en facteur mais je suis bloquée à

[Kabyle]

Je suis encore plus perdue qu'avant là

[Kabyle]

J'ai enfin réussi, merci à tous pour votre aide

[laetidom]

J'ai enfin réussi, merci à tous pour votre aide

Bonjour,

. . . et oui car

tout en sachant que le cours sur les identités remarquables nous dit que

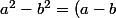[Kabyle]

Oui, merci