Bonjour, pourriez vous m'aider svp sur cette exo
Soient x1, ... , xp p éléments distincts de K. On considère l'ensemble F = { A appartient à K[X] / A(x1) = A(x2) = ... = A(xp) }
a) Montrer que F est un sous espace vectoriel de K[X] et que les éléments de F sont des polynômes de la forme (X-x1)(X-x2) ... (X-xp) Q + a où Q un polynôme et a une constante
b) Soit G = vect(X,X^2, ... , X^(p-1)) ; montrer que K[X] = F + G (en somme directe) (indication : effectuer la division euclidienne de P par (X-x1)(X-x2) ... (X-xp))
c) Quelle est la dimension de F inter Kn[X] ?
Polynôme et SEV
6 messages
- Page 1 sur 1
Re: Polynôme et SEV
Bonjour
D'abord il faudrait préciser que est un corps infini.
est un corps infini.
Je suppose que tu sais montrer que est un sous-espace vectoriel.
est un sous-espace vectoriel.
Ensuite, si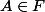 , pose
, pose 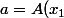=\cdots=A(x_p)) , et montre que
, et montre que 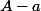 est divisible par
est divisible par ...(x-x_p))
D'abord il faudrait préciser que
Je suppose que tu sais montrer que
Ensuite, si
Re: Polynôme et SEV
salut
qui est P ?
Mikedz a écrit: (indication : effectuer la division euclidienne de P par (X-x1)(X-x2) ... (X-xp))
qui est P ?
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Polynôme et SEV
Salut,
Où pense tu que cela va être utile ?Mimosa a écrit:D'abord il faudrait préciser queest un corps infini.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Polynôme et SEV
Merci
Juste pour la dimension de F inter Kn[X] est ce que ca marche si j'utilise la formule de grassman ?
Juste pour la dimension de F inter Kn[X] est ce que ca marche si j'utilise la formule de grassman ?
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 74 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
