Existence même supllémentaire de deux sev

par **Daniel-Jackson** » 06 Oct 2007, 14:13

Salut la compagnie ,

Je cherche à démontrer que deux sous espaces vectoriels E1 et E2 d'un espace vectoriel E (de dimension finie) ont même supplémentaires si et seulement si ils ont même dimension . (lorsque le corps est infini ) .

J'ai un gros trou sur la première implication : même dimension ==> même suplémentaire . :stupid_in

Merci à vous .

par **yos** » 06 Oct 2007, 14:40

Bonjour.

Il faut le construire. Part d'une base

de

et complète là d'une part en une base

de

et d'autre part en une base

de

. Si tu mélanges tout tu obtiens une base de

(il faut juste montrer que le mélange est une partie libre) . Reste à complèter tout ça en une base de E.

par **Daniel-Jackson** » 06 Oct 2007, 15:10

Bonjour yos

Merci d'avoir répondu mais j'ai pas très bien compris .

En gros ce qu'on a fait c'est de construire une base de

et tu trouve un supplémentaire de ce dernier , mais c'est lequel le supplémentaire commun à

et à

?

Et si

?

par **Daniel-Jackson** » 06 Oct 2007, 15:47

Hop hop les amis , pour pas qu'on m'oublit :zen:

par **fahr451** » 06 Oct 2007, 16:04

bonjour

je te propose une autre approche
dim E = n
récurrence (descendante) sur p la dim commune

p = nrien à faire {0} convient

on suppose le résultat pour p >0
soit E1,E2 deux sev de dim p -1

E1UE2 n'est pas E car l'union n'est un supplémentaire que si l'un des deux est inclus dans l'autre et dans ce cas la réunion n'est pas E

il existe donc a dans E\E1UE2

on prend
E'1 = E1+ Ka et E'2 = E2+Ka les sommes sont directes

de dim p donc admettent un supllementaire commun H'

et on pose H = H' +ka qui est un supplémentaire de E1 et E2

par **Daniel-Jackson** » 06 Oct 2007, 16:07

Alors je pense avoir trouvé :

Soit

un supplémentaire de

.

On réitère en prenant :

On obtient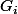

par récurrence .

Ces deux sous espaces ont même dimension à chaque fois et la dimension croit au fur et à mesure et comme elle est majoré par la dimension de E . On sait qu'à un moment ça s'arrête ça stationne et on aura gagné .

Le supplémentaire commun sera

.

Je pense que ça marche .

par **Daniel-Jackson** » 06 Oct 2007, 16:22

fahr451 a écrit:bonjour

je te propose une autre approche
dim E = n
récurrence (descendante) sur p la dim commune

p = nrien à faire {0} convient

on suppose le résultat pour p >0
soit E1,E2 deux sev de dim p -1

E1UE2 n'est pas E car l'union n'est un supplémentaire que si l'un des deux est inclus dans l'autre et dans ce cas la réunion n'est pas E

il existe donc a dans E\E1UE2

on prend
E'1 = E1+ Ka et E'2 = E2+Ka les sommes sont directes

de dim p donc admettent un supllementaire commun H'

et on pose H = H' +ka qui est un supplémentaire de E1 et E2

Ah merci fahr451

Ton raisonement me plait bien .

par **fahr451** » 06 Oct 2007, 16:27

merci moi aussi ça me plait bien
juste remplacer "supplémentaire " par sous espace à un moment
l'union est un sev que si ...

par **Daniel-Jackson** » 06 Oct 2007, 16:46

fahr451 a écrit:merci moi aussi ça me plait bien
juste remplacer "supplémentaire " par sous espace à un moment
l'union est un sev que si ...

Oui je me suis dit que c'était une petite faute de frappe , mais j'achète tout :happy2:

par **yos** » 06 Oct 2007, 17:07

Daniel-Jackson a écrit:En gros ce qu'on a fait c'est de construire une base de et tu trouve un supplémentaire de ce dernier , mais c'est lequel le supplémentaire commun à et à ?

Tu as la base

de

et tu la complètes en une base de E avec des vecteurs

.
Ensuite tu prends

et ce F vérifie ce que tu veux.

par **Daniel-Jackson** » 06 Oct 2007, 19:02

yos a écrit:Tu as la base de et tu là complètes en une base de E avec des vecteurs .
Ensuite tu prends et ce F vérifie ce que tu veux.

Oui je suis d'accord pour ce cas là , mais il y'a toujours le cas où E est de dimension paire et

et

en somme directe autrement dit le cas où

.

par **Daniel-Jackson** » 06 Oct 2007, 19:05

fahr451 a écrit:bonjour

je te propose une autre approche
dim E = n
récurrence (descendante) sur p la dim commune

p = nrien à faire {0} convient

on suppose le résultat pour p >0
soit E1,E2 deux sev de dim p -1

E1UE2 n'est pas E car l'union n'est un supplémentaire que si l'un des deux est inclus dans l'autre et dans ce cas la réunion n'est pas E

il existe donc a dans E\E1UE2

on prend
E'1 = E1+ Ka et E'2 = E2+Ka les sommes sont directes

de dim p donc admettent un supllementaire commun H'

et on pose H = H' +ka qui est un supplémentaire de E1 et E2

Salut farh451

J'ai voulu généraliser en suivant ta méthode lorsque j'ai

de même dimension . Parce que On a pas immédiatement le fait que La réunion d'espace vectoriels est un espace vectoriel que si y'en a un qui contient tout le monde .

Ou bien je me trompe ?

par **yos** » 06 Oct 2007, 19:16

Daniel-Jackson a écrit:Oui je suis d'accord pour ce cas là , mais il y'a toujours le cas où E est de dimension paire et et en somme directe autrement dit le cas où .

NON! Dans ce cas p=0 : ta base de

est

. Et il n'y a aucune raison d'aller chercher des cas particuliers pour le plaisir.

par **fahr451** » 06 Oct 2007, 19:23

Daniel-Jackson a écrit:Salut farh451

. Parce que On a pas immédiatement le fait que La réunion d'espace vectoriels est un espace vectoriel que si y'en a un qui contient tout le monde .

?

ben non ce n'est pas si immédiat à prouver

par **Daniel-Jackson** » 06 Oct 2007, 19:46

yos a écrit:NON! Dans ce cas p=0 : ta base de est . Et il n'y a aucune raison d'aller chercher des cas particuliers pour le plaisir.

Mes excuses , tu as entièrement raison :briques:

Merci pour votre aide à vous deux

par **Daniel-Jackson** » 06 Oct 2007, 19:47

fahr451 a écrit:ben non ce n'est pas si immédiat à prouver

Justement je disais que ce n'était pas immédiat . et d'ailleurs je me demande si c'est vrai .........?

par **Daniel-Jackson** » 06 Oct 2007, 20:40

Encore une petite question : Que faire si j'ai plus de deux sous espaces , car avec les deux méthodes ça coince à un moment ...

par **yos** » 06 Oct 2007, 21:27

Daniel-Jackson a écrit:Justement je disais que ce n'était pas immédiat . et d'ailleurs je me demande si c'est vrai .........?

Si c'est bien connu. Si aucun n'est inclus dans l'autre, tu prends x dans

et y dans

et tu peux constater que x+y n'est ni dans

ni dans

donc pas dans

(ça contredit le fait que

est un ev).

Pour le cas de plus de deux ev, c'est une bonne question. Je pense que les deux méthodes s'adaptent mais ça peut devenir lourd à écrire.

par **fahr451** » 06 Oct 2007, 21:45

en fait

il suffit de montrer que la réunion n'est pas E tout entier

pour K = R ou C
c'est évident chaque sev propre est d'intérieur vide donc la réunion aussi ce que n'est pas E

donc ma méthode s'adapte il existe a dans E\ E1U...UEk

et récurrence

si on veut montrer que la réunion de sous ev sans inclusion n'est pas un sev
c'est assez technique
récurrence et discussion de cas

par **Daniel-Jackson** » 06 Oct 2007, 22:41

fahr451 a écrit:en fait

il suffit de montrer que la réunion n'est pas E tout entier

pour K = R ou C
c'est évident chaque sev propre est d'intérieur vide donc la réunion aussi ce que n'est pas E

donc ma méthode s'adapte il existe a dans E\ E1U...UEk

et récurrence

si on veut montrer que la réunion de sous ev sans inclusion n'est pas un sev
c'est assez technique
récurrence et discussion de cas

Ah merci fahr

Excellent , rien à dire le coup de l'interieur vide bravo !
Si c'est pas indiscret , tu fais quoi dans la vie fahr ?
Parce que moi je vais passer l'agreg cette année et j'aimerais bien connaitre quelques ouvrages qui me permettraient d'acquérir un bon niveau à l'écrit .

En tout cas merci à vous

Existence même supllémentaire de deux sev

Existence même supllémentaire de deux sev

Qui est en ligne