Primitive

[Mouns688]

Bonjour ,

Je n'arrive pas à voir la méthode à suivre pour intégrer la fonction suivante :

(-1)/ ((x^2+1)^2)+c
En fait c'est sur le x^2 à l'intérieur de la parenthèse qui me pose un peu problème .

Je vous remercie par avance d'éclairer ma lanterne .

[zygomatique]

salut

déjà la constante on n'en a rien à péter puisque la dérivée d'une somme est la somme des dérivées

de même le coefficient - 1 on le jette à la poubelle (pour le moment) puisque la dérivée du produit d'une fonction par une constante est le produit de cette constante par la dérivée de la fonction ...

reste donc à trouver une primitive de la fonction

en lycée ... pas facile ...

au supérieur on ferait éventuellement le changement de variable x = sinh t

[Ben314]

Salut,
Il y a comme d'habitude des tas de méthodes.
Les méthodes "standards" consistent à faire des intégration par parties ou des changement de variable, mais à mon avis, la méthode la plus rapide, c'est décrire (sans en oublier...) les fonctions qui ont des dérivées "de ce type" là et d'essayer de reconstituer ta fonction par combinaisons linéaire.
Là, clairement qui a une dérivé du bon "type", il y a et mais y'a des truc en trop qu'on doit pouvoir éliminer grace au dérivées de et/ou .

Par contre, je pense pas que ce soit de niveau Lycée (actuel) vu qu'il y a quasi surement la fonction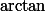 qui apparait dans les primitives de ta fonction.

[WillyCagnes]

bjr,

http://www.wolframalpha.com/input/?i=int1%2F(1%2Bx%5E2)%5E2

I=-1/2[x/(1+x²) +1/tan(x)]

[Mouns688]

Merci beaucoup les amis ,effectivement ça n'est pas du niveau lycée ,j'ai juste mal interprété mon exercice , du coup je vais tenter avec le changement de variable et la décomposition en éléments simple .

À bientôt