Sparthunter a écrit:D'accord donc la je dérive la fonction je fait ensuite une équation = 0 par la suite et j'aurai la valeurs de x
Dérive la fonction de degré 3 ===> tu obtiens donc une équation de degré 2, tu te dis alors quand est-ce que j'ai mon mini c'est quand j'ai une
tangente horizontale à
Cf, donc une droite horizontale donc celle-ci ayant une pente nulle donc une dérivée nulle ===> équation de degré 2 de la dérivée = 0 =====> ax² + bx + c = 0
====>
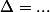
+ solutions . . . ou bien avec le programme . . . (pour contrôler) car sur une copie, si rien n'est indiqué sur la nature du résultat, on attend la valeur littérale !
Tu dois arriver à :

Bon courage, tu n'es pas loin ! . . .

