Calcul de limite

[SeifMaths]

Bonjour,
En 3/b, j'essaye de calculer la dérivé à gauche mais je bloque en

(pi/2 moins)
Aussi pour justifier la dérivabilité à gauche, il faut d'abord calculer la limite non?


PS: Il y a une petite erreur dans 3-a je crois, il doit y avoir C(Pi/2) = au lieu de g(Pi/2)

[Lostounet]

Salut,
Quels sont les outils que tu connais pour le calcul des limites?
La règle de L'Hopital? Les développements de Taylor? Aucun des deux?

[SeifMaths]

Salut,
Quels sont les outils que tu connais pour le calcul des limites?
La règle de L'Hopital? Les développements de Taylor? Aucun des deux?

Seulement La règle de L'Hopital, j'ai essayé de l'appliquer mais je n'y arrive pas dans ce cas

[Lostounet]

=



Puis tu utilises le fait que sin(y)/y tend vers 1 (tu peux le justifier avec L'Hopital) lorsque y tend vers 0 et tu fais tendre tout le monde vers pi/2.

[SeifMaths]

=



Puis tu utilises le fait que sin(y)/y tend vers 1 (tu peux le justifier avec L'Hopital) lorsque y tend vers 0 et tu fais tendre tout le monde vers pi/2.

Merci!

[Ben314]

Salut,
Perso, je trouve que vous faîtes bien compliqué (mais c'est peut-être pas mal comme entrainement...) :
Pour tout vu que sur l'intervalle.
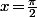
Et, comme en on a (par définition de ) c'est qu'en fait on a pour tout .
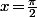
Et vu sous cette forme, la fonction est clairement continue et dérivable en (et on calcule la dérivée, y compris en , on ne peut plus bêtement avec du (u/v)'=...)

P.S. Et avec un soupçon de formules trigo, on peut même vérifier que pour tout .