Vérification de calcul limite please :)
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Lacouille
- Membre Naturel
- Messages: 31
- Enregistré le: 02 Oct 2010, 13:47
-
 par Lacouille » 11 Nov 2010, 18:47
par Lacouille » 11 Nov 2010, 18:47
Je vous dérange pour une dernière fois, juste pour que vous me disiez si mon calcul est juste ou pas :
f(x)=
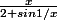
Determiner
-\left(\frac{x}{2}\right)\right])
3)a)
-\frac{x}{2}=\frac{x}{2+\sin\,\frac{1}{x}}-\frac{x}{2}=-\frac{x\,\sin\,\frac{1}{x}}{2(2+\sin\,\frac{1}{x})})
-\frac{x}{2}=-\frac{\frac{\sin\,\frac{1}{x}}{\frac{1}{x}}}{2(2+\sin\,\frac{1}{x})})
Or

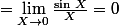
d' où
-\left(\frac{x}{2}\right)\right]=0)
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 11 Nov 2010, 18:57
par Arnaud-29-31 » 11 Nov 2010, 18:57
Lacouille a écrit: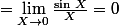
Il y a une erreur ici ...
-
Lacouille
- Membre Naturel
- Messages: 31
- Enregistré le: 02 Oct 2010, 13:47
-
 par Lacouille » 11 Nov 2010, 19:02
par Lacouille » 11 Nov 2010, 19:02
c'est indéterminé ...... car c'est de la forme
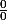
??
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 11 Nov 2010, 19:05
par Arnaud-29-31 » 11 Nov 2010, 19:05
Oui,
Si je te dis que
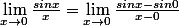
, ca te dit quelque chose ?
Si non, c'est aussi égal à
 - sin0}{x})
-
Lacouille
- Membre Naturel
- Messages: 31
- Enregistré le: 02 Oct 2010, 13:47
-
 par Lacouille » 11 Nov 2010, 19:06
par Lacouille » 11 Nov 2010, 19:06
Taux d'accroissement??
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 11 Nov 2010, 19:07
par Arnaud-29-31 » 11 Nov 2010, 19:07
Limite d'un taux d'accroissement ... ca fait penser à quoi ?
-
Lacouille
- Membre Naturel
- Messages: 31
- Enregistré le: 02 Oct 2010, 13:47
-
 par Lacouille » 11 Nov 2010, 19:09
par Lacouille » 11 Nov 2010, 19:09
Si le taux d'accroissement à une limite finie quand x tend vers a, on note f'(a) cette limite finie et on dit que f' est dérivable en a
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 11 Nov 2010, 19:12
par Arnaud-29-31 » 11 Nov 2010, 19:12
Ici a c'est 0 et f c'est sin donc notre limite est égale à quoi ?
-
Rebelle_
- Membre Irrationnel
- Messages: 1383
- Enregistré le: 27 Aoû 2010, 18:04
-
 par Rebelle_ » 11 Nov 2010, 19:15
par Rebelle_ » 11 Nov 2010, 19:15
Hello ! =)
En fait Arnaud essaye de te montrer une manière de calculer exactement la limite que tu cherches - qui a priori semble relever de l'indétermination.
On a
 = \frac{g(x) - g(0)}{x-0})
où g(x) = sin(x). Dans ton cours tu dois avoir quelque chose qui te dit que
 - g(0)}{x-0} = g'(0))
, or ici g'(x) = ... et donc g'(0) = ..., et de fait
}{x} = ...)

NB : tu n'oublieras pas de parler de la dérivabilité de f et g

-
Lacouille
- Membre Naturel
- Messages: 31
- Enregistré le: 02 Oct 2010, 13:47
-
 par Lacouille » 11 Nov 2010, 19:16
par Lacouille » 11 Nov 2010, 19:16
à 0 car

=

= 0
-
Rebelle_
- Membre Irrationnel
- Messages: 1383
- Enregistré le: 27 Aoû 2010, 18:04
-
 par Rebelle_ » 11 Nov 2010, 19:17
par Rebelle_ » 11 Nov 2010, 19:17
Tu es sûr de ce que tu nous dis là ? :)
-
Lacouille
- Membre Naturel
- Messages: 31
- Enregistré le: 02 Oct 2010, 13:47
-
 par Lacouille » 11 Nov 2010, 19:18
par Lacouille » 11 Nov 2010, 19:18
A d'accord oui je vois merci à tous les 2 et bonne continuation à vous :lol3:
-
Lacouille
- Membre Naturel
- Messages: 31
- Enregistré le: 02 Oct 2010, 13:47
-
 par Lacouille » 11 Nov 2010, 19:19
par Lacouille » 11 Nov 2010, 19:19
Rebelle_ a écrit:Tu es sûr de ce que tu nous dis là ?

Nan je finissait mon calcul d'avant que j'ai foiré donc c'est faux

-
Rebelle_
- Membre Irrationnel
- Messages: 1383
- Enregistré le: 27 Aoû 2010, 18:04
-
 par Rebelle_ » 11 Nov 2010, 19:19
par Rebelle_ » 11 Nov 2010, 19:19
Ah tu as compris ?!
Bon très bien, merci et bonne continuation à toi aussi !
=)
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 11 Nov 2010, 19:20
par Arnaud-29-31 » 11 Nov 2010, 19:20
Arnaud-29-31 a écrit:Si non, c'est aussi égal à
 - sin0}{x})
Bon on va remplace le x par h :
 - sin0}{h} = ... ??)
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 11 Nov 2010, 19:21
par Arnaud-29-31 » 11 Nov 2010, 19:21
Ahh

donc ca fait quoi ??
Maintenant la même avec

... ^^
-
Rebelle_
- Membre Irrationnel
- Messages: 1383
- Enregistré le: 27 Aoû 2010, 18:04
-
 par Rebelle_ » 11 Nov 2010, 19:24
par Rebelle_ » 11 Nov 2010, 19:24
Tu es en train de balancer deux des questions de mon dernier DS... :P
Si tu veux M. le posteur (je suis une fille sage =P) je peux te donner les autres pour t'entraîner ;)
-
Lacouille
- Membre Naturel
- Messages: 31
- Enregistré le: 02 Oct 2010, 13:47
-
 par Lacouille » 11 Nov 2010, 19:28
par Lacouille » 11 Nov 2010, 19:28
Je trouve que ma limite = 1 c'est normal ??(Je parle de ma limite que je cherche, celle de f(x)-x/2)
-
Lacouille
- Membre Naturel
- Messages: 31
- Enregistré le: 02 Oct 2010, 13:47
-
 par Lacouille » 11 Nov 2010, 19:30
par Lacouille » 11 Nov 2010, 19:30
Rebelle_ a écrit:Tu es en train de balancer deux des questions de mon dernier DS...

Si tu veux M. le posteur (je suis une fille sage =P) je peux te donner les autres pour t'entraîner

C'est bien gentil mais entre moi et les maths, c'est pas une belle histoire. Moins j'en fais, mieux je me porte :lol3:
-
Rebelle_
- Membre Irrationnel
- Messages: 1383
- Enregistré le: 27 Aoû 2010, 18:04
-
 par Rebelle_ » 11 Nov 2010, 19:34
par Rebelle_ » 11 Nov 2010, 19:34
Lacouille a écrit:C'est bien gentil mais entre moi et les maths, c'est pas une belle histoire. Moins j'en fais, mieux je me porte :lol3:
Héhéhé moi aussi ;D
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 82 invités