Bonjour, j'ai des équations différentielles à résoudre, je voudrai savoir si mon résultat est juste
1) y'=-(y-1)^3
je trouve solution constante y=-1
solution non constante y= 1+√1/2t
j'ai pris t comme variable
2) y'=cosxcosy/siny
y=arccos(e^(1/4)*cos^2+c)
merci pour votre aide
Equations diff d'ordre 1
5 messages
- Page 1 sur 1
Re: equations diff d'ordre 1
bonjour
methode classique......
tu derives ton resultat et tu regardes si l'equation differentielle est verifiée
methode classique......
tu derives ton resultat et tu regardes si l'equation differentielle est verifiée
Re: equations diff d'ordre 1
salut
y <> 1 ...
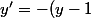^3 <=> \dfrac {-2(y - 1)'}{(y - 1)^3} = 1 <=> \dfrac 1 {(y - 1)^2} = t + k) avec k constante réelle ...
avec k constante réelle ...
y <> 1 ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: equations diff d'ordre 1
c'est évidemment un  ... ou alors écrire
... ou alors écrire
zygomatique a écrit:salut
y <> 1 ...avec k constante réelle ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
