Bonjour,
Je fais un exercice et je bloque.
g(x) = ( 1 + e^(-x) )^1/2.
I =] 1 , 2 [
1) Démontrer que pour tout x appartenant à I, g(x) appartient à I.
2) Démontrer que pour tout x appartenant à I, 0 ≤ | g'(x)| ≤ 1/2e ≤ 1/5.
Si quelqu'un a une idée merci.
Fonction et interval
6 messages
- Page 1 sur 1
Re: Fonction et interval
musique137 a écrit:Bonjour,
Je fais un exercice et je bloque.
g(x) = ( 1 + e^(-x) )^1/2.
I =] 1 , 2 [
1) Démontrer que pour tout x appartenant à I, g(x) appartient à I.
2) Démontrer que pour tout x appartenant à I, 0 ≤ | g'(x)| ≤ 1/2e ≤ 1/5.
Si quelqu'un a une idée merci.
Salut,
C'est du niveau supérieur ça?
Si x dans ]1;2[ alors
1<x<2
-2<-x<-1
Par croissance de exp sur R
Exp(-2)<exp(-x)<exp(-1)
1+exp(-2)<...<...
Par croissance de la racine sur R+...
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Fonction et interval
Bonjour,
Merci de la réponse rapide. Oui je suis tout à fait d'accord mais comment savoir sans calculatrice
que ( 1 + exp (-2) ) ^1/2 < 2 ?
Ensuite pour la dérivé j'ai g'(x) = exp (-x) / 2 (1 + exp (-x) ) ^1/2.
En faisant les inéquations j'obtiens :
1 / 2 ( 1 + exp (-1) ) ^1/2 < 1 / 2 ( 1 + exp (-x) ) ^1/2 < 1 / 2 ( 1 + exp (-2) ) ^1/2
Mais je ne sais pas comment faire après pour rajouter exp(x) qu'il me manque pour retrouver g'(x)
Merci de la réponse rapide. Oui je suis tout à fait d'accord mais comment savoir sans calculatrice
que ( 1 + exp (-2) ) ^1/2 < 2 ?
Ensuite pour la dérivé j'ai g'(x) = exp (-x) / 2 (1 + exp (-x) ) ^1/2.
En faisant les inéquations j'obtiens :
1 / 2 ( 1 + exp (-1) ) ^1/2 < 1 / 2 ( 1 + exp (-x) ) ^1/2 < 1 / 2 ( 1 + exp (-2) ) ^1/2
Mais je ne sais pas comment faire après pour rajouter exp(x) qu'il me manque pour retrouver g'(x)
Re: Fonction et interval
musique137 a écrit:Bonjour,
Merci de la réponse rapide. Oui je suis tout à fait d'accord mais comment savoir sans calculatrice
que ( 1 + exp (-2) ) ^1/2 < 2 ?
)
On peut toujours partir sur
1 + exp (-2) ) ^1/2 < 2
Équivaut à
(Car tout est positif)
1+exp(-2) <4
Exp(-2)<3
1/exp(2)<3
Qui est toujours vrai
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Fonction et interval
hello,
 = \frac{1}{2e^x\sqrt{1+e^{-x}}})
g' est décroissante, donc sur I, g'(1) est le max et g'(2) le min.
Les valeurs absolues c'est easy puisque g' est positive sur R de toute facon.
La minoration par 0 pareil pour les même raisons
pour le majorant,

avec U > 1 or en particulier pour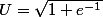 > 1
> 1
donc)
g' est décroissante, donc sur I, g'(1) est le max et g'(2) le min.
Les valeurs absolues c'est easy puisque g' est positive sur R de toute facon.
La minoration par 0 pareil pour les même raisons
pour le majorant,
avec U > 1 or en particulier pour
donc
la vie est une fête 
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 18 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
