Bonjour,
je dois donner la forme explicite de Un avec comme donnée : Un+1 = 1/(1+Un) et U0= alpha
Ma piste était telle mais elle n'est pas correcte :
Un= ((n-1)+(n-2)*alpha) / ((n+1)+(n-1)*alpha)
Elle fonctionne pour les certains des termes mais pas tous, je ne sais pas comment trouver la forme correcte de Un. Merci d'avance pour votre aide
Expression de Un
11 messages
- Page 1 sur 1
Re: Expression de Un
Bonjour,
Calculer U1, U2, U3 pour un début de récurrence sur Un=(1+alpha)/(n+(n-1)alpha).
A vérifier...
Calculer U1, U2, U3 pour un début de récurrence sur Un=(1+alpha)/(n+(n-1)alpha).
A vérifier...
Re: Expression de Un
Salut,
Montre par récurrence que, pour tout entier naturel , on a
, on a \!=\!\dfrac{a_n\alpha\!+\!b_n}{c_n\alpha\!+\!d_n}) et trouve les relations de récurrences entre les différents termes (tu devrait rapidement tomber sur la suite dite "de Fibonacci"...)
et trouve les relations de récurrences entre les différents termes (tu devrait rapidement tomber sur la suite dite "de Fibonacci"...)
Sinon, si tu as vu la notion d'homographie et son lien avec les matrices 2x2, tu peut passer par là, ça raccourcirait les calculs...
Montre par récurrence que, pour tout entier naturel
Sinon, si tu as vu la notion d'homographie et son lien avec les matrices 2x2, tu peut passer par là, ça raccourcirait les calculs...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Expression de Un
Dasson2 a écrit:Bonjour,
Calculer U1, U2, U3 pour un début de récurrence sur Un=(1+alpha)/(n+(n-1)alpha).
A vérifier...
Cela ne fonctionne par pour U1, avec ton expression : U1=1+U0 or en réalité avec l'expression de la suite U1=1/(1+U0)
Re: Expression de Un
Ben314 a écrit:Salut,
Montre par récurrence que, pour tout entier naturel, on a
et trouve les relations de récurrences entre les différents termes (tu devrait rapidement tomber sur la suite dite "de Fibonacci"...)
Sinon, si tu as vu la notion d'homographie et son lien avec les matrices 2x2, tu peut passer par là, ça raccourcirait les calculs...
Ta réponse est en effet três pertinante, je ne comprends juste pas comment mettre la suite de fibonnaci a l'interieur de l'expression de Un
Re: Expression de Un
salut
peut-être faudrait-il calculer u_{n + 1}(a) en fonction de u_n(a) ...
peut-être faudrait-il calculer u_{n + 1}(a) en fonction de u_n(a) ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Expression de Un
Bonjour,
Ma réponse donnée : pour n>1.
Mais est-ce nécessaire ?
De telles suites définies par récurrence peuvent être étudiées avec des dessins comme
http://rdassonval.free.fr/flash/suitef.jpg
copie d'écran d'une adaptation rapide d'un de mes programmes.
Ce programme peut être adapté à ton énoncé.
Les questions pourraient être :
suite non monotone,
limite égale à (racine(5)-1)/2, environ 0.618 ??
Ma réponse donnée : pour n>1.
Mais est-ce nécessaire ?
De telles suites définies par récurrence peuvent être étudiées avec des dessins comme
http://rdassonval.free.fr/flash/suitef.jpg
copie d'écran d'une adaptation rapide d'un de mes programmes.
Ce programme peut être adapté à ton énoncé.
Les questions pourraient être :
suite non monotone,
limite égale à (racine(5)-1)/2, environ 0.618 ??
Re: Expression de Un
La théorie dit que si  et
et  sont les éléments doubles (ici racines de
sont les éléments doubles (ici racines de 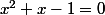 ) la relation s'écrit
) la relation s'écrit 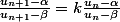 .
.  n'est pas très difficile à calculer, d'où ...
n'est pas très difficile à calculer, d'où ...
Re: Expression de Un
Bonjour,
J'ai essayé de donner une réponse abordable au lycée mais j'ai vu que c'était du "supérieur" ; en effet...
Une solution à vérifier est proposée sur cette copie d'écran modifiée
http://rdassonval.free.fr/flash/suitef.jpg
Merci de m'avoir aidé à passer le temps.
Bon amusement au questionneur, s'il lit les réponses...
J'ai essayé de donner une réponse abordable au lycée mais j'ai vu que c'était du "supérieur" ; en effet...
Une solution à vérifier est proposée sur cette copie d'écran modifiée
http://rdassonval.free.fr/flash/suitef.jpg
Merci de m'avoir aidé à passer le temps.
Bon amusement au questionneur, s'il lit les réponses...
Re: Expression de Un
A mon avis, ce qui était attendu, c'est
- Soit de dire que, si alors
alors \alpha\!+\!(b_n\!+\!d_n)}) ce qui signifie que l'on peut par exemple prendre
ce qui signifie que l'on peut par exemple prendre 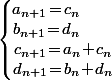 avec
avec  donc par exemple
donc par exemple  .
.
Donc ;
;  et, pour tout
et, pour tout 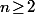 on a
on a  : la suite
: la suite _{n\geq 0}) est la classique suite de Fibonnacci : (0,1,1,2,3,5,8,13,21,34,55,89,...)
est la classique suite de Fibonnacci : (0,1,1,2,3,5,8,13,21,34,55,89,...)
Ensuite, ;
;  et, pour tout
et, pour tout 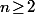 on a
on a  donc en fait
donc en fait  pour tout
pour tout  et on a donc
et on a donc  pour tout
pour tout 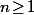 .
.
- Soit plus simplement de calculer les 5 ou 6 premiers termes pour voir très clairement apparaitre la fameuse suite en question puis démontrer le résultat çi dessus par récurrence.
Ensuite, concernant l'éventuelle écriture de en fonction de
en fonction de  , je pense que ça a forcément déjà été fait.
, je pense que ça a forcément déjà été fait.
Sinon, si on connait un tant soit peu le calcul matriciel, face aux 4 formules de récurrence çi dessus, il doit venir à l'esprit de poser) de façon à écrire les fameuses relations sous la forme
de façon à écrire les fameuses relations sous la forme  avec
avec ) et
et  .
.
On a adonc et la route est toute tracée : il faut diagonaliser
et la route est toute tracée : il faut diagonaliser  pour l'écrire
pour l'écrire  avec
avec  diagonale pour obtenir
diagonale pour obtenir  .
.
On eut remarquer que le dont parle Pythalés correspondant en fait au changement de base induit par
dont parle Pythalés correspondant en fait au changement de base induit par  , son
, son  est le polynôme caractéristique de
est le polynôme caractéristique de  et son
et son  est le rapport entre les deux valeurs propres de
est le rapport entre les deux valeurs propres de  .
.
- Soit de dire que, si
Donc
Ensuite,
- Soit plus simplement de calculer les 5 ou 6 premiers termes pour voir très clairement apparaitre la fameuse suite en question puis démontrer le résultat çi dessus par récurrence.
Ensuite, concernant l'éventuelle écriture de
Sinon, si on connait un tant soit peu le calcul matriciel, face aux 4 formules de récurrence çi dessus, il doit venir à l'esprit de poser
On a adonc
On eut remarquer que le
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Expression de Un
@Ben314
Merci pour toutes ces précisions qui m'ont fait rajeunir (je suis en retraite depuis ... longtemps).
J'ai essayé de répondre à la question du questionneur et propose une solution abordable au lycée dans la copie d'écran que je viens d'actualiser.
Merci pour toutes ces précisions qui m'ont fait rajeunir (je suis en retraite depuis ... longtemps).
J'ai essayé de répondre à la question du questionneur et propose une solution abordable au lycée dans la copie d'écran que je viens d'actualiser.
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 8 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
