Devoir math
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Nonam3
- Messages: 4
- Enregistré le: 21 Déc 2016, 13:44
-
 par Nonam3 » 21 Déc 2016, 13:50
par Nonam3 » 21 Déc 2016, 13:50
un prof m a donner un exercice su ça:
trouver les nombres réels dont le double est égal a leur cube .Bien sur en tant que bon matheux feignant j'ai trouver les reponses mais n ayant pas suivit le cours je sus bien embêter pour formuler le tout
HELP


-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 21 Déc 2016, 13:57
par Lostounet » 21 Déc 2016, 13:57
Soit x un tel nombre
Tu cherches x tel que 2x=x^3
C'est si compliqué? :p
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
Nonam3
- Messages: 4
- Enregistré le: 21 Déc 2016, 13:44
-
 par Nonam3 » 21 Déc 2016, 14:08
par Nonam3 » 21 Déc 2016, 14:08
oui ok moi aussi je l ai fait ça mais apres??????
-
Nonam3
- Messages: 4
- Enregistré le: 21 Déc 2016, 13:44
-
 par Nonam3 » 21 Déc 2016, 14:08
par Nonam3 » 21 Déc 2016, 14:08
Nonam3 a écrit:oui ok moi aussi je l ai fait ça mais apres??????
bon sang de bon soir
-
Nonam3
- Messages: 4
- Enregistré le: 21 Déc 2016, 13:44
-
 par Nonam3 » 21 Déc 2016, 14:09
par Nonam3 » 21 Déc 2016, 14:09
en plus ça répond pas a ma question

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 21 Déc 2016, 14:10
par Lostounet » 21 Déc 2016, 14:10
Ramène tout d'un côté puis factorise par x...
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 21 Déc 2016, 19:03
par zygomatique » 21 Déc 2016, 19:03
Nonam3 a écrit:un prof m a donner un exercice su ça:
trouver les nombres réels dont le double est égal a leur cube .Bien sur en tant que
bon matheux feignant j'ai trouver les reponses mais n ayant pas suivit le cours je sus bien embêter pour formuler le tout
HELP

MDR les mots bon et feignant sont évidemment contradictoires ...
et la suite du fil me prouve que l'un des deux est faux ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Internaute
- Membre Naturel
- Messages: 39
- Enregistré le: 21 Déc 2016, 19:50
-
 par Internaute » 21 Déc 2016, 21:22
par Internaute » 21 Déc 2016, 21:22
Les deux nombres réels répondant à la propriété voulue par le prof auquel vous faîte référence sont 2^0,5 (à prononcer "racine carré de deux") et -(2^0,5) (à prononcer "moins racine carré de deux")

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 21 Déc 2016, 21:28
par chan79 » 21 Déc 2016, 21:28
Internaute a écrit:Les deux nombres réels répondant à la propriété voulue par le prof auquel vous faîte référence sont 2^0,5 (à prononcer "racine carré de deux") et -(2^0,5) (à prononcer "moins racine carré de deux")
pas d'accord !

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 21 Déc 2016, 21:49
par Lostounet » 21 Déc 2016, 21:49
Internaute a écrit:Les deux nombres réels répondant à la propriété voulue par le prof auquel vous faîte référence sont 2^0,5 (à prononcer "racine carré de deux") et -(2^0,5) (à prononcer "moins racine carré de deux")
Merci de ne pas balancer des solutions toutes faites... ce n'est pas la politique du forum.Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
Internaute
- Membre Naturel
- Messages: 39
- Enregistré le: 21 Déc 2016, 19:50
-
 par Internaute » 23 Déc 2016, 08:44
par Internaute » 23 Déc 2016, 08:44
chan79 a écrit: Internaute a écrit:Les deux nombres réels répondant à la propriété voulue par le prof auquel vous faîte référence sont 2^0,5 (à prononcer "racine carré de deux") et -(2^0,5) (à prononcer "moins racine carré de deux")
pas d'accord !
J'ai bien vérifié, et la racine carré de 2 est bel et bien la moitié de son propre cube

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 23 Déc 2016, 08:52
par chan79 » 23 Déc 2016, 08:52
Salut
L'équation
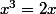
admet 3 solutions
-
Internaute
- Membre Naturel
- Messages: 39
- Enregistré le: 21 Déc 2016, 19:50
-
 par Internaute » 23 Déc 2016, 09:09
par Internaute » 23 Déc 2016, 09:09
DELETED
Modifié en dernier par
Internaute le 23 Déc 2016, 09:34, modifié 2 fois.
-
Internaute
- Membre Naturel
- Messages: 39
- Enregistré le: 21 Déc 2016, 19:50
-
 par Internaute » 23 Déc 2016, 09:23
par Internaute » 23 Déc 2016, 09:23
chan79 a écrit:En divisant par

, tu laisses échapper une solution...
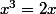
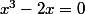
=0)
(x+\sqrt{2})=0)
L'ensemble des solutions est {

}
C'est juste.
Merci d'avoir rectifié mon erreur.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités
, tu laisses échapper une solution...
}