Volume integral triple
10 messages
- Page 1 sur 1
Volume integral triple
Bonjour je me retrouv encore face a deux problèmes ou jai de la difficilte a borner. Je doit trouver le volume du solide entre y^2+z^2=4x, x=3, y^2=x. Et le volume du solide limite par les plans coordonees et.le plan x+y+z=1 avec la triple integral de 1/(x+y+z+1)^(3). Mes recherches sur le net ont ete tres infructueuse merci.
Re: Volume integral triple
Salut,
La notion de "solide entre ...", mathématiquement parlant, ça veut évidement rien dire du tout.
Souvent (en particulier ici), les équations derrière le "entre", ça correspond à des "surfaces" (sans rentrer trop dans le détail de ce qu'on va appeler "surface") et, si on les représente dans R^3, ces surfaces "coupent" l'espace R^3 et délimitent différentes "régions".
S'il y a une et une seule de ces "régions" qui est bornée, c'est en général cette région là qu'on considère comme étant "le solide entre ..." (ce qui signifie en fait qu'on considère qu'un "solide", ça a pas le droit d'être non borné)
Ici, l'équation est celle d'un Cône de révolution avec son sommet en (0,0,0) et qui "s'ouvre indéfiniment" dans la direction de l'axe des x (du coté x>0).
est celle d'un Cône de révolution avec son sommet en (0,0,0) et qui "s'ouvre indéfiniment" dans la direction de l'axe des x (du coté x>0).
L'équation x=3 est celle d'un plan qui coupe le cône suivant un cercle et donc, si on regarde juste ces deux équation, la notion de "solide entre les deux" semble parfaitement défini vu que les surfaces délimitent une unique région bornée correspondant à et
et  (si tu préfère, une autre façon de voir les choses, c'est que si on prenais des inégalités autres que celle là, par exemple
(si tu préfère, une autre façon de voir les choses, c'est que si on prenais des inégalités autres que celle là, par exemple  et
et  ou bien
ou bien  et
et  , on aurait une région de l'espace non bornée)
, on aurait une région de l'espace non bornée)
Le problème, c'est qu'il y a la troisième équation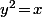 qui correspond à une surface qui coupe la région çi dessus en deux "sous régions" évidement toute les deux bornées donc je ne vais aucune raison particulière de privilégier une des deux "région" par rapport à l'autre, c'est à dire que je ne vois aucune raison de privilégier l'inégalité
qui correspond à une surface qui coupe la région çi dessus en deux "sous régions" évidement toute les deux bornées donc je ne vais aucune raison particulière de privilégier une des deux "région" par rapport à l'autre, c'est à dire que je ne vois aucune raison de privilégier l'inégalité  par rapport à
par rapport à  .
.
Et en plus, même les deux premières équations, c'est pas évident que mon interprétation soit bonne vu qu'on pourrait aussi commencer par voir ce que donne la première et la troisième surface...
Bref, pour te donner un exemple bien plus simple car en dimension 2, si on te demandait quelle est l'aire de la surface du plan située entre x=1 ; y=1 ; x+y=1 et y=2x, tu répondrait quoi (fait un dessin pour comprendre où se situe le problème).
EDIT : j'ai dit n'importe quoi, y²+z²=4x, c'est pas un cône de révolution donc il faut revoir les arguments (mais je suis pas sûr que ça change grand chose à la conclusion, c'est à dire qu'on peut pas savoir qui est le fameux "solide" en question)
Ou alors c'est que c'est pas du tout le volume du solide que tu veut calculer, mais l'intégrale de la fonction 1/(x+y+z+1)^3 prise sur le domaine délimité par les plans x=0, y=0, z=0 et x+y+z=1 ?
La notion de "solide entre ...", mathématiquement parlant, ça veut évidement rien dire du tout.
Souvent (en particulier ici), les équations derrière le "entre", ça correspond à des "surfaces" (sans rentrer trop dans le détail de ce qu'on va appeler "surface") et, si on les représente dans R^3, ces surfaces "coupent" l'espace R^3 et délimitent différentes "régions".
S'il y a une et une seule de ces "régions" qui est bornée, c'est en général cette région là qu'on considère comme étant "le solide entre ..." (ce qui signifie en fait qu'on considère qu'un "solide", ça a pas le droit d'être non borné)
Ici, l'équation
L'équation x=3 est celle d'un plan qui coupe le cône suivant un cercle et donc, si on regarde juste ces deux équation, la notion de "solide entre les deux" semble parfaitement défini vu que les surfaces délimitent une unique région bornée correspondant à
Le problème, c'est qu'il y a la troisième équation
Et en plus, même les deux premières équations, c'est pas évident que mon interprétation soit bonne vu qu'on pourrait aussi commencer par voir ce que donne la première et la troisième surface...
Bref, pour te donner un exemple bien plus simple car en dimension 2, si on te demandait quelle est l'aire de la surface du plan située entre x=1 ; y=1 ; x+y=1 et y=2x, tu répondrait quoi (fait un dessin pour comprendre où se situe le problème).
EDIT : j'ai dit n'importe quoi, y²+z²=4x, c'est pas un cône de révolution donc il faut revoir les arguments (mais je suis pas sûr que ça change grand chose à la conclusion, c'est à dire qu'on peut pas savoir qui est le fameux "solide" en question)
Et ça, non seulement ça risque aussi d'être ambigüe (comme l'autre), mais en plus je comprend même pas ce que ça peut vouloir dire "un solide délimité par une intégrale"Veelox a écrit:Et le volume du solide limite par les plans coordonees et.le plan x+y+z=1 avec la triple integral de 1/(x+y+z+1)^(3). Mes recherches sur le net ont ete tres infructueuse merci.
Ou alors c'est que c'est pas du tout le volume du solide que tu veut calculer, mais l'intégrale de la fonction 1/(x+y+z+1)^3 prise sur le domaine délimité par les plans x=0, y=0, z=0 et x+y+z=1 ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Volume integral triple
Pour évite toute ambiguïté je vais ecrire les questions comme elle sont littéralement presente : trouvez le volume du solide delimite par les surfaces y^2+z^2=4x, x=3 et inferieur a y^2=x et evaluer lintegral suivante : triple integral 1/(x+y+z+1)^3 dV ou V est le volume delimite par les plans coordonees et le plan x+y+z=1.
Re: Volume integral triple
Veelox a écrit:...y^2+z^2=4x, x=3 et inferieur a y^2=x...
Je comprend pas. Tu pourrais pas l'écrire proprement (avec du mimetex par exemple) ?
De nouveau, je comprend rien.Veelox a écrit:Évaluer l'integrale suivante : triple intégral 1/(x+y+z+1)^3 dV ou V est le volume délimite par les plans coordonnes et le plan x+y+z=1.
Parmi les trucs qui ressemblerais vaguement à ton bidule, il me vient à l'esprit :
1) Déterminer l'intégrale
2) Déterminer le volume
Et ni dans un cas, ni dans l'autre il n'y a un truc style dV où V serait un "volume" : si un tel truc a du sens, c'est éventuellement en physique, mais comme je ne connais pas le sens que ça a, je ne peut pas t'aider...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Volume integral triple
Effectivement, désolé, mais je peut pas t'aider.
- Je sais pas ce que ça veut dire un solide "intérieur à" une équation (au fond, je sais pas si je préférais pas ce que tu avais écrit plus haut, à savoir "inférieur à" qui n'a rien à voir avec "intérieur à" mais qui donnait l'impression qu'on avait affaire à une inégalité...)
- Je comprend pas le sens que ça peut avoir une intégrale sur V avec du dV à la fin.
Par contre, là où je suis catégorique, c'est que un truc du style "...le volume limité par...", ça a pas de sens.
En math., le mot volume, ça s'emploie sous la forme "le volume de quelque chose" donc le truc proche qui aurait du sens, c'est "le volume du solide délimité par..."
Regarde le lien WIKI sur "volume" si tu n'est pas convaincu.
P.S. C'est quoi comme bouquin ?
- Je sais pas ce que ça veut dire un solide "intérieur à" une équation (au fond, je sais pas si je préférais pas ce que tu avais écrit plus haut, à savoir "inférieur à" qui n'a rien à voir avec "intérieur à" mais qui donnait l'impression qu'on avait affaire à une inégalité...)
- Je comprend pas le sens que ça peut avoir une intégrale sur V avec du dV à la fin.
Par contre, là où je suis catégorique, c'est que un truc du style "...le volume limité par...", ça a pas de sens.
En math., le mot volume, ça s'emploie sous la forme "le volume de quelque chose" donc le truc proche qui aurait du sens, c'est "le volume du solide délimité par..."
Regarde le lien WIKI sur "volume" si tu n'est pas convaincu.
P.S. C'est quoi comme bouquin ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Volume integral triple
Cest un livre de note de cours ecrit par un de mes professeur que lom utilise en classe mais je suis au Quebec moi donc cest peut etre nos petite différence de vulgarisation
Re: Volume integral triple
Je veut bien tenter une interprétation, mais attention, c'est sans garantie...
Pour le 1), je suis à peu prés persuadé que, concernant les deux premières équation, il faut comprendre et
et  (c.f. post précédent concernant le "pourquoi").
(c.f. post précédent concernant le "pourquoi").
Concernant la troisième équation, je suis nettement moins sûr de mon coup, mais si on me demande où est "l'intérieur" de la parabole (du plan) d'équation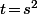 , je pense que je répondrait que c'est les (s,t) tels que
, je pense que je répondrait que c'est les (s,t) tels que  . Donc là, j'aurais tendance à penser que la troisième équation, elle est à prendre sous la forme
. Donc là, j'aurais tendance à penser que la troisième équation, elle est à prendre sous la forme  .
.
Ensuite, le tout est de mettre ces 3 inégalités sous une forme "exploitable" pour du calcul d'intégrale :
- Première solution : varie de 0 à 3, puis, pour
varie de 0 à 3, puis, pour  connu,
connu,  varie de
varie de 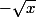 à
à  , puis pour
, puis pour  et
et  connus,
connus,  varie de
varie de  à
à  donc le volume du solide, c'est
donc le volume du solide, c'est 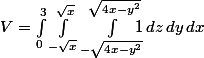
Mais ça semble pas facile à calculer (en particulier il faudra trouver une primitive de ...)
...)
- Deuxième solution : La même chose, mais en changeant l'ordre d'intégration donc (par exemple) en commençant par regarder où se situe indépendamment de
indépendamment de  et
et  , mais ça risque de ne pas être mieux (i.e. avec des racines qui font c...)
, mais ça risque de ne pas être mieux (i.e. avec des racines qui font c...)
- Troisième solution : Utiliser un changement de variable (à condition que tu ait vu comment ça marche avec le jacobien et tout et tout) et on peut soit en utiliser un "classique" (sphérique, cylindrique, etc...) soit en fabriquer un "adapté" au problème. Là, le truc qui semble adapté, c'est du cylindrique en prenant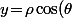) ;
; 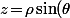) puis, pour paramétrer, considérer
puis, pour paramétrer, considérer  puis
puis  puis
puis  (en distinguant deux cas selon que
(en distinguant deux cas selon que |\!\leq\!\frac{1}{2}) ou pas.
ou pas.
Pour le 2), la seule interprétation qui me semble plausible, c'est la première du post précédent (l'intégrale sur V avec du dV à la fin me laisse plus que perplexe, mais je vois pas d'autre possibilité sur ce que ça pourrait vouloir dire écrit correctement).
Dans ce cas, la région est claire : c'est
est claire : c'est  et je pense qu'à peu prés toute les méthode vont marcher :
et je pense qu'à peu prés toute les méthode vont marcher :
- Soit une paramétrisation directe : varie de 0 à 1, puis, pour
varie de 0 à 1, puis, pour  connu,
connu,  varie de
varie de  à
à  , puis pour
, puis pour  et
et  connus,
connus,  varie de
varie de  à
à 
- Soit un changement de variable en posant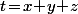 (et je sais pas quoi pour les deux autres variables : à voir...)
(et je sais pas quoi pour les deux autres variables : à voir...)
Pour le 1), je suis à peu prés persuadé que, concernant les deux premières équation, il faut comprendre
Concernant la troisième équation, je suis nettement moins sûr de mon coup, mais si on me demande où est "l'intérieur" de la parabole (du plan) d'équation
Ensuite, le tout est de mettre ces 3 inégalités sous une forme "exploitable" pour du calcul d'intégrale :
- Première solution :
Mais ça semble pas facile à calculer (en particulier il faudra trouver une primitive de
- Deuxième solution : La même chose, mais en changeant l'ordre d'intégration donc (par exemple) en commençant par regarder où se situe
- Troisième solution : Utiliser un changement de variable (à condition que tu ait vu comment ça marche avec le jacobien et tout et tout) et on peut soit en utiliser un "classique" (sphérique, cylindrique, etc...) soit en fabriquer un "adapté" au problème. Là, le truc qui semble adapté, c'est du cylindrique en prenant
Pour le 2), la seule interprétation qui me semble plausible, c'est la première du post précédent (l'intégrale sur V avec du dV à la fin me laisse plus que perplexe, mais je vois pas d'autre possibilité sur ce que ça pourrait vouloir dire écrit correctement).
Dans ce cas, la région
- Soit une paramétrisation directe :
- Soit un changement de variable en posant
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Volume integral triple
En effet je connais les coordonnees cylindrique, spherique et le jacobien, par contre pour en ''fabrique'' un je connais pas du tout et pour le 2ieme effectivement cetai ma borne en z qui etait mauvaise jai pu le reussir.
Re: Volume integral triple
Pour la question 1
en calculant
et en multipliant le résultat par 4, j'arrive à
s'il s'agit bien de la zone qui contient le point (1,0,0)
à vérifier
en calculant
et en multipliant le résultat par 4, j'arrive à
s'il s'agit bien de la zone qui contient le point (1,0,0)
à vérifier
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

