J'ai un dm de maths sur exponentielle et je n'ai pas très bien compris certaines questions :
II- Etude géométrique
On définit une application exp C --> C
f (z) = e^R(z) e^i*I(z) appelée exponentielle complexe. Si z appartient à C, on note exp(z) = e^z. On note T la transformation du plan qui au point M d'affixe z associé le point M' d'affixe e^z.
1.Soit k appartenant a R. On note Dk la droite d'équation x=k, et Dk l'ensemble des affixes des points de Dk.
a. En raisonnant par double inclusion, montrer que Dk = {k + iy, y appartenant a R}
b. Déterminer l'image de Dk par exp
c. En déduire l'image de la droite Dk par T. Que trouve-t-on pour k=0 ?
d. Sur un même graphique, tracer D-1 et T(D-1) en noir
D0 et T(D0) en vert et D1 et T(D1) en rouge.
Je n'ai pas tout compris...
Pourriez vous m'aider ?
Merci d'avance
Exponentielle complexe
4 messages
- Page 1 sur 1
Re: exponentielle complexe
salut
voir : http://www.ilemaths.net/sujet-exponenti ... 16467.html
1/ quel est l’intérêt de raisonner par double inclusion
qu'est-ce que la droite d'équation x = k (géométriquement) ?
ensuite on a tout simplement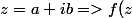 = e^z = e^a e^{ib})
voir : http://www.ilemaths.net/sujet-exponenti ... 16467.html
1/ quel est l’intérêt de raisonner par double inclusion
qu'est-ce que la droite d'équation x = k (géométriquement) ?
ensuite on a tout simplement
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: exponentielle complexe
la droite x = k est la droite parallèle à l'axe des ordonnées passant par k.
Re: exponentielle complexe
la droite d'équation x = k est l'ensemble des points M d'abscisse k ...
c'est donc aussi l'ensemble des points M de coordonnées (k, y) ... ou d'affixe k + iy avec y variant dans R
c'est donc aussi l'ensemble des points M de coordonnées (k, y) ... ou d'affixe k + iy avec y variant dans R
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 20 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
