Déterminer matrice A

[rik1895]

bonsoir,

j'aurai besoin d'un coup de main afin de determiner une matrice, voici l'enoncé de l'exo :

Soit A une matrice carrée symetrique d'ordre quatre telle que :
x transposé fois A fois x = x1² +x2² +(x3+x4)² + x4²

1) determiner A
2) on pose b transposé = ( 1 1 2 3), reoudre Ax = b par la methode de choleky

pour la question 2 je pense que je n'aurai aucun mal a la faire une fois A determiner mais je n'ai aucune idée de comment resoudre la premiere question ... tout ce que je peu faire c'est determiner la matrice que j'appele C associé a x transposé fois A fois x mais comment determiner A a partir de la ?

pourriez vous me montrer la marche a suivre svp ?

Merci

[Ben314]

Salut,
Le fait que, partant uniquement de la connaissance de la forme quadratique on puisse retrouver la matrice (symétrique) A, ça provient au fond de ce qu'on appelle "les formules de polarisation".
Ça te rappelle quelque chose ?

Sinon, avec un peu de bon sens, on peut directement "lire" la matrice A dans l'expression x1² +x2² +(x3+x4)² + x4², mais évidement, il faut savoir ce qu'on cherche...
Si tu veut le faire "en lecture directe", tu n'as qu'à écrire avec plein de lettres puis calculer et tu comprendra comment on fait pour "lire" les coef. de A dans le résultat.

[rik1895]

Merci pour ta réponse Ben,

Alors en suivant la 2eme solution que tu proposes je trouve ( sauf erreur de calcul ) : a = 1, b = 0, c= 0, d=0, e=1, f=0, g=0, h=1, i=1, j=2

[Ben314]

Oui, c'est ça.
Et ça se lit directement dans la forme développée de x1² +x2² +(x3+x4)² + x4².
Les termes diagonaux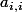 de A sont les coeffs. devant les.
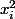Les autres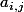 (avec 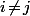) sont égaux à la moitié du coeff. qu'il y a devant le 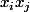(le 1/2 venant du fait que le même 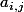apparait 2 fois dans la matrice)