Bonsoir,
Je suis entrain de travailler sur le sujet de l'ENASS 2015, et l'une des questions consiste à trouver la limite de la fonction f(x) quand x tend vers 1. f(x) = (1-x^-n)/ racine de (x-1) . Je n'arrive pas à faire disparaître la forme indéterminée, je ne sais pas par quelles transformations il faut passer.
Voilà, merci, bonne soirée !
Limites de fonctions prépa
6 messages
- Page 1 sur 1
Re: Limites de fonctions prépa
Bonsoir,
Pour lever une indétermination, que donnent les bonnes vieilles méthodes que sont les développements limités et la règle de l'Hôpital ?
Pour lever une indétermination, que donnent les bonnes vieilles méthodes que sont les développements limités et la règle de l'Hôpital ?
Re: Limites de fonctions prépa
Bonsoir,
Je ne vois pas du tout ce que sont ces méthodes je ne me souviens pas l'avoir vu en TS
Je ne vois pas du tout ce que sont ces méthodes je ne me souviens pas l'avoir vu en TS
Re: Limites de fonctions prépa
salut
 = \dfrac {1 - x^{-n}}{\sqrt {x - 1}} = - \dfrac {1^{-n} - x^{-n}}{1 - x} \dfrac {x - 1}{\sqrt {x - 1} - \sqrt {1 - 1}})
...
...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Limites de fonctions prépa
Bonsoir,
As-tu vu les développements limités ? je suppose que non, si tu te réfères au programme de TS.
Dans ce cas, tu peux transformer en
en  , puis remarquer que
, puis remarquer que 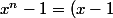 (x^{n-1}+...+1)) .
.
As-tu vu les développements limités ? je suppose que non, si tu te réfères au programme de TS.
Dans ce cas, tu peux transformer
Re: Limites de fonctions prépa
zygomatique a écrit:salut
...
ouais suite au msg de pseuda encore plus simple
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 59 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
