Equivalence
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Laure22
- Messages: 4
- Enregistré le: 18 Sep 2016, 09:23
-
 par Laure22 » 18 Sep 2016, 09:29
par Laure22 » 18 Sep 2016, 09:29
Bonjour,
1) Définition négligeabilité + résoudre un exemple => Fait
2) Définition équivalence + résoudre un exemple => Fait
Les questions qui me posent problème sont les suivantes:
3) Donner un exemple de deux suites (Un) et (Vn) équivalentes telles que n²+Un et n²+Vn ne soient pas équivalentes.
J'ai cherché avec différents Un et Vn mais ensuite je retombe toujours sur une nouvelle équivalence.
4) (Un) et (Vn) sont non nulles et équivalentes à xn et yn respectivement, justifier que UnVn est équivalente à xnyn.
En gros je dois faire une démonstration mais c'est un point du cours que je ne comprends pas trop.
Merci d'avance!

-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 18 Sep 2016, 09:46
par jlb » 18 Sep 2016, 09:46
3) essaie (3 - n²) et (1-n²)
4) dans ton cours, c'est quoi la définition de suite équivalente: commence par traduire que (xn) et (un) sont équivalentes, que (yn) et (vn) sont équivalentes et ce que tu dois obtenir (xnyn) équivalente à (unvn)
-
Laure22
- Messages: 4
- Enregistré le: 18 Sep 2016, 09:23
-
 par Laure22 » 18 Sep 2016, 10:36
par Laure22 » 18 Sep 2016, 10:36
3) Effectivement, problème résolu! J'étais partie dans bien plus compliqué!
4)Si j'ai bien compris je dois dire:
♦ Si Un ~xn alors il existe alpha(n) →1 (n→+ inf) telle que pour n assez grand: Un= alpha(n)xn <=> Un/xn=alpha(n) (car Un non nulle). Idem pour Vn ~yn.
♦ Un*Vn= alpha(n)xn*beta(n)yn ~ xnyn car lim alpha(n) → 1 (n→ +inf) et lim beta(n) → 1 (n→+inf)
-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 18 Sep 2016, 10:50
par jlb » 18 Sep 2016, 10:50
Oui c'est l'idée, après, la rédaction est à améliorer. Bon courage.

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 18 Sep 2016, 13:19
par zygomatique » 18 Sep 2016, 13:19
salut
4/ je ne vois pas pourquoi la condition sur les suites u et v (non nulles) ... mais bon faut voir la def qui t'a été donnée sur les équivalences)
je ne mets pas les indices n
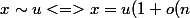))
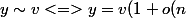))
donc
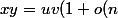)(1 + o(n)) = uv(1 + o(n) + o(n) + o(n)o(n)) = uv(1 + o(n)))
...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités

