Bonjour,
J'ai un exercice où je dois étudier les variations d'une fonction et donc procéder avec un tableau de signe de la fonction dérivée puis donner les variations. Mais cette fonction me parait assez complexe et j'aurais besoin d'aide.
f(x)=(1)/(x²+1)^4
et la dérivée de cette fonction me donne : -8x(x²+1)^3 / (x²+1)^8
Mais je ne sais pas comment étudier le signe du dénominateur et du nominateur.
Les puissance de 3 et de 8 me bloque, si quelqu'un peut m'expliquer comment ça marche ce serait très sympa.
merci d'avance.
Variations de fonction f
8 messages
- Page 1 sur 1
Re: variations de fonction f
Bonjour,
Oui, tu as le droit de simplifier ainsi.
Mais de toutes façons n'est-il pas toujours strictement positif ?
n'est-il pas toujours strictement positif ?
Oui, tu as le droit de simplifier ainsi.
Mais de toutes façons
Re: variations de fonction f
Au contraire c'est toujours strictement positif. C'est la dérivée qui est strictement négative.samoufar a écrit:Bonjour,
Oui, tu as le droit de simplifier ainsi.
Mais de toutes façonsn'est-il pas toujours strictement positif ctement strictement ?
Re: variations de fonction f
Du coup j'ai -8x/ (x²+1)^5
je sais déterminer le signe de -8x mais comment je fait pour (x²+1)^5 ? C'est toujours positif sur - infini + infini ?
je sais déterminer le signe de -8x mais comment je fait pour (x²+1)^5 ? C'est toujours positif sur - infini + infini ?
Re: variations de fonction f
salut
 = \dfrac 1 {(x^2 + 1)^4})
f est définie sur R et paire ( <=> f(-x) = f(x) ))
sur l'intervalle [0, +oo[ les fonctions :
 et
et 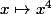 sont croissantes donc
sont croissantes donc ^4) est croissante
est croissante
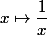 est décroissante donc
est décroissante donc }) est décroissante
est décroissante
par parité on en déduit ce qui se passe su ]-oo, 0]
...
f est définie sur R et paire ( <=> f(-x) = f(x) ))
sur l'intervalle [0, +oo[ les fonctions :
par parité on en déduit ce qui se passe su ]-oo, 0]
...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: variations de fonction f
Non, cela dépends deJAx a écrit:Du coup j'ai -8x/ (x²+1)^5
je sais déterminer le signe de -8x mais comment je fait pour (x²+1)^5 ? C'est toujours positif sur - infini + infini ?
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 70 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
