Résolution de système

[lrnt00]

Bonjour, j'ai un soucis avec mon système:
{y=(-2a+4)x+a^2+3
{y=(-2b+4)x+b^2+3
Je suis bloque à l'étape suivante:
{(-2a+4)x+a^2+3-y=0
{y=(-2b+4)x+b^2+3
Enfaite c'est le -y qui me gêne avec la règle des signes. Si vous pouvez m'aider!

[Razes]

Fais la soustraction des deux premières équations du système, ainsi c'est ramené à une équation d'une seule inconnues.

[Pisigma]

Bonjour,

Perso je ferai plutôt ainsi:




(1)-(2) membre à membre va te donner

Tu peux facilement tirer x , d'où y en remplaçant dans (1) ou(2)

[lrnt00]

Oui mais est-ce que je met des parenthèses quand je remplace y par l'équation? C'est ça qui me bloque parce que sinon ça change les signes

[Razes]

Commence par faire le calcul, je t'ai mis sur la voie et Pisigma t'a donné un grand coup de main.

[lrnt00]

J'ai trouvé
x=( -a^2+b^2)/x(-2a+2b)
Je sais pas comment simplifier

[Razes]

J'ai trouvé
x=( -a^2+b^2)/x(-2a+2b)
Je sais pas comment simplifier

Alors, je ne sais pas d'où vient tout ça.

Pisigma t'a gentillement mâché le travail et tu l'as avalé de travers.

Tu as l'équation :


Elle est de la forme , comment résous tu une équation du 1er degré? Et qu'elles sont les conditions pour les solutions?

[lrnt00]

Ah bah je suis navré mais je suis perdu là. J'ai trouvé Comme pisigma sauf que j'ai isolé le x:
x(-2a+2b)-b^2+a^2=0
x(-2a+2b)=-a^2+b^2
EST ce que je jusque là ça va ou je fais une erreur?

[Razes]

Oui, c'est bon jusqu'à là. Pourquoi tu change l'ordre des termes inutilement?

[Razes]

Disons que c'est ça.
, c'est de la forme 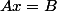que peux tu dire à propos de sa résolution?

[zygomatique]

salut

avant de diviser il faut savoir par quoi on divise ... et en particulier surtout pas par 0 ...

2(a - b)x = a² - b² <=> (a - b)(2x - a - b) = 0

... et on retourne au collège ...

[Razes]

En 4ème

[lrnt00]

Bon,
Je souhaite trouver x, donc je divise:
x(-2a+2b)=(-a^2+b^2)
x= (-a^2+b^2)/(-2a+2b)
Ça ne se fait pas?
Je ne divise pas par 0 là.

[Razes]

Connais tu a et b?
Dans quel cas la quantité par laquelle tu divise est nulle?

[lrnt00]

Non

[lrnt00]

La quantité est nulle lorsque y a 0?

[Razes]

Au collège tu n'a pas résolu l'équation du style ?

[lrnt00]

Mais si! Mais pour moi c'est pas ce que j'ai là! Je vois pas le truc, je passe à côté de quelque chose là c'est pour ça que je demande de l'aide, j'ai sûrement oublier une "règle du Collège" mais de là à ne pas savoir résoudre 2x=4..

[Razes]

Erègle générale nous avons:
Équations du premier degré:

Soit et deux nombres entiers relatifs tels que n'est pas nul.
Résoudre l'équation du premier degré :
, consiste à trouver l'inconnue .

Comme n'est pas nul, nous pouvons diviser par a chaque côté de l'équation. Ce qui donne :
, soit

Dans ton cas, tu as:
, donc et
On va distinguer les cas suivants:
1)
Dans ce cas Donc la solution est
2) Donc la solution est

[lrnt00]

Ah bah voilà c'est la factorisation qui me manquait! En tout cas merci à tous pour vos réponses!