Limite des suites

[rubi]

Bonjour,

Quelles sont les limites pour les suites arithmétiques et géométriques. Comment est ce qu'on les trouve théoriquement (sans le graphique et simplement avec les formules) :

Suite arithmétique :
tn = t1 +(n-1).r
Sn =n/2 +( t1+tn )

Suite géométrique :
tn = t1 .(r^(n-1))
Sn = t1 ((1-r^n)/(1-r))

merci

[zygomatique]

salut

si u(n) = an + b alors u(n) = f(n) avec f(x) = ax + b et on connaît les limites d'une fonction affine à l'infini

donc la limite d'une suite arithmétique est l'infini ....

si (n + 1) = qu(n) alors il suffit de savoir ce qui se passe quand on multiplie une quantité par un nombre q

si b = aq alors |b| < |a| si et seulement si |q| < 1 et |b| > |a| si et seulement si |q| > 1

...

[rubi]

Je comprends ce que vous dites à l'exception de (n+1) = qu(n). D'où vient-il ?

Ensuite, une suite peut également converger vers un réel, non ?

[zygomatique]

ben pour une suite géométrique ....

ben oui ...

mais dans le cas des suites géométriques ce ne peut être que 0 ...

[Lostounet]

Pour une suite géométrique, on peut partir du constat suivant:

si on multiplie 0.1 par 0.1, on trouve 0.01 (nombre encore plus petit):

...
Cela signifie que, plus on multiplie 0.1 par lui-même, et plus on trouve un nombre petit, proche de 0:

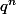tend donc vers 0 lorsque q = 0.1 (mais aussi quel que soit q compris entre -1 < q < 1, c'est pareil)

Par contre si q = 2, tu verras que q^n tend vers + l'infini

Et si q = -1 par exemple, alors q^n n'a pas de limite ! (elle vaut tantôt -1, tantôt 1...)

[zygomatique]

il fut un temps où au collège on apprenait (par soi-même) que :





puis ensuite on le voyais en seconde explicitement ....

maintenant un terminale n'est plus capable de le montrer ...

[rubi]

Lostounet :
Merci à vous pour vos explications. J'ai eu du mal à comprendre car mon professeur ne m'a pas expliqué avec les même connotations mais j'ai essayé de m'habituer et c'est plus compréhensible. Un grand merci