Matrice

[Prepa_S]

Bonjour,

je souhaite obtenir de l'aide s'il vous plait afin de déterminer a et b de façon à ce que la matrice vaut certaine valeur

Enoncé;

soit M= [en 1ère ligne : a b
en 2nd ligne: a b ]

déterminer a et b tels que M²=0 , M²=I

Pour M²=0 j'ai trouvé pour a=1 et b=-1
mais je ne sais pas comment procéder pour M²=1 ce qui signifie qu'a cette matrice j'aurai des diagonales égales à 1

pourriez vous m'aider svp?

[zygomatique]

salut

dans M² = I

I désigne la matrice identité ... quelle est sa définition ?

[Prepa_S]

salut

dans M² = I

I désigne la matrice identité ... quelle est sa définition ?

la matrice identité veut dire que la matrice aura une diagonale de 1 et les autres coefficients seront nuls

[aymanemaysae]

Bonjour;

Pour le plaisir de voir la forme des matrices quand il s'agit d'un exercice de matrices, j'essaierai de réécrire l'énoncé:

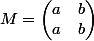, ce qui donne pour 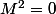(au lieu de 0 , je préfère représenter la matrice nulle par ) .

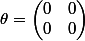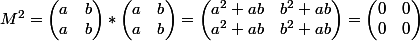, donc ...... ?

Pour l'autre cas je préfère écrire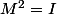 avec la matrice identité représentée par , on a donc 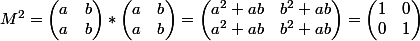, donc ...... ?

[Archytas]

Sinon il y a une méthode sans calcul :Si il existe a,b tels que M²=I ça implique quoi sur l'inversibilité de M ? Conclusion ?

[aymanemaysae]

Bonjour;

j'aime beaucoup ces méthodes de résolution qui arrivent à leur fin sans calculs et seulement par des déductions logiques: j'essaierai de m'entraîner pour avoir ce coup d’œil, même si je suis sûr et certain que c'est un don.

Merci pour le tuyau .

[Prepa_S]

Bonjour;

Pour le plaisir de voir la forme des matrices quand il s'agit d'un exercice de matrices, j'essaierai de réécrire l'énoncé:

, ce qui donne pour (au lieu de 0 , je préfère représenter la matrice nulle par ) .

, donc ...... ?

Pour l'autre cas je préfère écrire avec la matrice identité représentée par , on a donc , donc ...... ?

veuillez m'excuser pour ce gene. merci de votre aide

[Prepa_S]

Sinon il y a une méthode sans calcul :Si il existe a,b tels que M²=I ça implique quoi sur l'inversibilité de M ? Conclusion ?

je ne comprends pas ce que vous voulez dire mais merci de votre aide

[aymanemaysae]

Bonjour;

je ne vais pas interférer sur la méthode de M. Archytas, mais pour ma méthode qui ne contient aucune subtilité, surtout pour le cas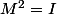 (matrice identité), l'égalité entre les deux matrices

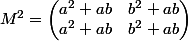et et surtout entre la première colonne de 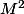et la première colonne de la matrice identité nous donne que 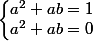ce qui est absurde,

donc il n'y a pas de matrice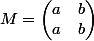 telle que .

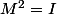Je vous laisse maintenant méditer sur la méthode de M. Archytas qui est très subtil et agréable à rédiger.

[Prepa_S]

Bonjour;

je ne vais pas interférer sur la méthode de M. Archytas, mais pour ma méthode qui ne contient aucune subtilité, surtout pour le cas (matrice identité), l'égalité entre les deux matrices

et et surtout entre la première colonne de et la première colonne de la matrice identité nous donne que ce qui est absurde,

donc il n'y a pas de matrice telle que .

Je vous laisse maintenant méditer sur la méthode de M. Archytas qui est très subtil et agréable à rédiger.

Merci bien pour votre aide

[aymanemaysae]

Pour la méthode de M. Archytas, je vous donne une indication (ceci parce que vous êtes un camarade des classes préparatoires: classes prépas) :

On a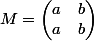 , donc 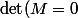(matrice avec deux colonnes identiques),

et comme vous cherchez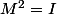 (matrice identité) donc , donc , ce qui est différent de , donc on ne peut avoir de telle matrice.

Merci M. Archytas.

[Prepa_S]

Pour la méthode de M. Archytas, je vous donne une indication (ceci parce que vous un camarade des classes préparatoires: classes prépas) :

On a , donc (matrice avec deux colonnes identiques),

et comme vous cherchez (matrice identité) donc , donc , ce qui est différent de , donc on ne peut avoir de telle matrice.

Merci M. Archytas.

Merci pour l'indication

[Ben314]

Sinon il y a une méthode sans calcul :Si il existe a,b tels que M²=I ça implique quoi sur l'inversibilité de M ? Conclusion ?

Y'a même mieux que sans calculs : tu attend deux petites heures et aymanemaysae te met la solution toute cuite et tu as même pas besoin de réfléchir : juste recopier...

[capitaine nuggets]

Salut à tous !


Objectivement, je viens de regarder la discussion et je ne peux pas donner tort à Ben314 n'a pas tort : merci aymanemaysae de relire (si nécessaire) le règlement du forum, laisser réfléchir la personne, et essayer de privilégier les indications à l'avenir plutôt que de déballer une solution.



Entre autre, tu aurais pu le laisser faire les calculs et te contenter de donner des indications, comme par exemple qu'il suffisait de calculer telle ou telle quantité, puis de résoudre telle ou telle équation, etc....

[aymanemaysae]

Bonjour;

Je demande pardon à M.Ben314 et M. Capitaine Nuggets, mais il m'arrive beaucoup de me mettre à la place de l'initiateur du fil et d'avoir un peu de compassion (même un peu trop) quand je ressens qu'il est désorienté ou qu'il manque des rudiments pour arriver à terme.

Ceci dit, je m'abstiendrai dorénavant d'intervenir avant les quarante huit heures qui suivent l'initiation du fil pour ne pas créer de désagréments à personne. De plus quand je donne ma version de la solution, je ne dis pas que c'est LA SOLUTION: je ne suis qu'un élève de classes préparatoires (les résultats du CNC n'ont pas encore été publiés) et j'ai toujours besoin de l'avis d'un professeur sur ce que je rédige comme démonstration.

[lulu math discovering]

Pour revenir sur la méthode d'Architias, j'ai compris ce qu'il voulait insinuer sur l'inversibilité de M, mais je ne vois pas plus loin

[aymanemaysae]

Bonsoir;

J'essaierai de suivre les conseils de M. capitaine Nuggets, et je dirai:

1) Une matrice A est inversible si et seulement si son déterminant est non nul.
2) Quelque soient les matrices carrées d'ordre n , A et B telles que AB = I (matrice identité), alors A et B sont inversibles et chacune d'elles est l'inverse de l'autre.

donc , comme déterminant de M est ...... et M^2 = I alors ...... .

[Archytas]

Même sans passer par le déterminant, M² = I implique que M est inversible, M a deux colonnes égales donc n'est pas inversible. Donc M² = I n'a pas de solution.

[lulu math discovering]

Ok merci.