Serie convergente

[foufa2]

bonjour tout le monde,

j'ai une question concernant les series.

soit une suite qui converge vers a.
et soit s > a,
est ce que la serie
est converege ?
je pense que oui, pouviez vous m'aider?

[samoufar]

Bonjour,

Ton intuition est correcte Je te donnes cependant quelques petites indications :

• Si , alors que se passe-t-il à partir d'un certain rang pour les termes de la suite ?
  
  
• Est-ce qu'on peut en déduire une majoration convenable de (au moins à partir d'un certain rang) ?

Si tu ne trouves toujours pas, n'hésites pas à demander plus d'indications

[foufa2]

pour
alors

et on a



comme ca peut on dire que la serie et convergente?

[samoufar]

Ton idée de découper la somme en deux est pertinente, tu es sur la bonne voie. Néanmoins il reste quelques "réglages " à faire :

• Au départ, tu prends donc la série est divergente et ne constitue donc pas une bonne majoration ;
  
  
• Attention, la suite converge vers et non vers . Par conséquent tu dois plutôt écrire
  
  
  
  (pas besoin de la valeur absolue, seule cette inégalité nous intéressera puisqu'on cherche une majoration) ;

Aussi, je te donne quelques indications supplémentaires :

• Est-ce qu'on ne peut pas trouver une valeur de intéressante ? Par exemple en trouvant une valeur de qui traduit la propriété "les sont plus proches de que de "
  
  
• N'oublies pas le résultat que tu veux obtenir : tu veux trouver tel que, à partir d'un certain rang on ait
  
  .

N'hésites pas si tu bloques toujours

[foufa2]

merci pour ton aide, j'essaierai de trouver cette

[foufa2]

on a alors

il existe

pour
et par consequence
par suite

la demonstration est correcte maintenant ?

[samoufar]

Prends juste au lieu de pour avoir (nécessaire pour la définition de la limite). Sinon c'est tout bon

Au passage, pour éviter de t'encombrer avec des en plus des autres paramètres, tu peux prendre par exemple , ça fait moins de lettres dans les calculs

[foufa2]

Merci ,
J'ai une autre question,
si
reste le resultat encore vrai?

[samoufar]

A partir d'un certain rang tu as et tu en déduis une majoration convenable. Donc ça marche

Edit : Mon argument ne marche pas (voir mon post suivant)...

[foufa2]

peut tu m'expliquer plus?,
voila comment je peut voire la limite superieure,
.

[samoufar]

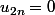
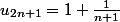
Au temps pour moi, ma remarque était erronée (il suffit de considérer la suite définie par et par exemple).

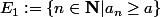
Par contre, une autre façon de faire serait de découper ta somme en deux parties (1), à savoir en sommant sur puis sur .

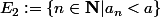
Pour , la majoration est simple à trouver

Pour , tu peux dire qu'à partir d'un certain rang, tous les termes sont suffisament proches de (mieux : la suite converge vers (2)) pour trouver une bonne majoration (ça revient exactement au même que le cas précédent).

Remarques

(1) : Etant donné qu'on ne peut pas se permettre de découper des sommes de série comme on veut, pour rédiger ça proprement, tu peux partir de la fin, c'est-à-dire travailler sur chacune des sommes séparément, montrer que tout est bien convergent puis regrouper les deux sommes.

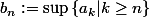
(2) : Pour montrer ça proprement tu peux par exemple considérer la suite définie par et travailler à l'aide d'encadrements

[foufa2]

Merci beaucoup pour ton aide , Mais je n'ai pas compris une chose dans la deuxieme etape: comment peut on montrer que la suite est convergente? et comment je peux utiliser la suite .. je sais que cette suite est decroissante et que

[samoufar]

NB : Bien évidemment ceci est valable lorsque est infini. Si est fini alors on a affaire à une somme finie, qui ne pose aucun problème


Maintenant si est infini alors pour tout , on a (par définition de et de ).

On a mieux concernant la suite : elle converge vers (décroissante, minorée et on connait sa borne inférieure, qui est sans aucun doute sa limite).

Donc par passage à la limite (théorème "des gendarmes") : ...

La conclusion est alors la même que le cas traité au début du fil.

[foufa2]

Merci beaucoup samoufar pour ton aide