Série convergente vers 1-1/e
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mbj335
- Membre Naturel
- Messages: 13
- Enregistré le: 16 Mai 2012, 12:59
-
 par mbj335 » 16 Mai 2012, 13:06
par mbj335 » 16 Mai 2012, 13:06
Bonjour,
Je suis à la recherche de séries convergentes vers 1-1/e (ou de fonctions tendant vers cette valeur à l'infini).
Si vous en connaissez des familles je suis preneur !
Objectif : Je m'amuse avec le théorème de Fermat (a^n + b^n = c^n)
-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
 par MacManus » 16 Mai 2012, 14:15
par MacManus » 16 Mai 2012, 14:15
Bonjour,
Wolfram indique quelques séries
icienfin rien de bien incroyable...
-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
 par MacManus » 16 Mai 2012, 14:43
par MacManus » 16 Mai 2012, 14:43
On a par exemple la suite de fonctions suivante, pour tout x de [0;1]:
}=\frac{ne^{x-1}}{n+x})
avec
}dx=\Bigint_{0}^{1}e^{x-1}dx=1-\frac{1}{e})
-
mbj335
- Membre Naturel
- Messages: 13
- Enregistré le: 16 Mai 2012, 12:59
-
 par mbj335 » 16 Mai 2012, 14:43
par mbj335 » 16 Mai 2012, 14:43
Merci c'est bien aimable, en fait les séries données convergent vers 1/e en combinant avec des séries convergente vers 1 je dois y arriver.
-
mbj335
- Membre Naturel
- Messages: 13
- Enregistré le: 16 Mai 2012, 12:59
-
 par mbj335 » 16 Mai 2012, 14:48
par mbj335 » 16 Mai 2012, 14:48
MacManus a écrit:On a par exemple la suite de fonctions suivante, pour tout x de [0;1]:
}=\frac{ne^{x-1}}{n+x})
avec
}dx=\Bigint_{0}^{1}e^{x-1}dx=1-\frac{1}{e})
Ah oui ces fonctions sont peut-être plus intéressantes...merci
-
mbj335
- Membre Naturel
- Messages: 13
- Enregistré le: 16 Mai 2012, 12:59
-
 par mbj335 » 16 Mai 2012, 15:51
par mbj335 » 16 Mai 2012, 15:51
Malheureusement les fonctions
}=\frac{ne^{x-1}}{n+x})
n'ont pas de primitives simples donc difficile d'exprimer la limite en fonction de n sans trainer l'intégrale...
-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
 par MacManus » 16 Mai 2012, 22:54
par MacManus » 16 Mai 2012, 22:54
mbj335 a écrit:Malheureusement les fonctions
}=\frac{ne^{x-1}}{n+x})
n'ont pas de primitives simples donc difficile d'exprimer la limite en fonction de n sans trainer l'intégrale...
oui très juste, il faut trouver autre chose alors.

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 16 Mai 2012, 23:04
par fatal_error » 16 Mai 2012, 23:04
pourquoi pas la serie géométrique
somme (1-e/(e-1))^k
avec 1-e/(e-1)<1
la vie est une fête

-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
 par MacManus » 16 Mai 2012, 23:35
par MacManus » 16 Mai 2012, 23:35
fatal_error a écrit:pourquoi pas la serie géométrique
somme (1-e/(e-1))^k
avec 1-e/(e-1)<1
Yo,
ouais c'est pas bête du tout, mais dans ce cas j'aurais mis plutôt
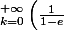^k)
, avec

-
mbj335
- Membre Naturel
- Messages: 13
- Enregistré le: 16 Mai 2012, 12:59
-
 par mbj335 » 16 Mai 2012, 23:48
par mbj335 » 16 Mai 2012, 23:48
mbj335 a écrit:Malheureusement les fonctions
}=\frac{ne^{x-1}}{n+x})
n'ont pas de primitives simples donc difficile d'exprimer la limite en fonction de n sans trainer l'intégrale...
En fait je crois que ce sont les fonctions que je cherche...j'obtiens de bons résultats pour la conjecture de Fermat, je sens que c'est le bon angle...si

j'ai deja pu montrer que soit
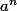
soit
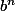
est borné par
.dx).c^n)
...
-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
 par MacManus » 17 Mai 2012, 00:12
par MacManus » 17 Mai 2012, 00:12
Et quel lien fais-tu entre les entiers du théorème de Fermat et les séries ou suites de fonctions convergeant vers 1-(1/e) ?
-
mbj335
- Membre Naturel
- Messages: 13
- Enregistré le: 16 Mai 2012, 12:59
-
 par mbj335 » 17 Mai 2012, 10:22
par mbj335 » 17 Mai 2012, 10:22
MacManus a écrit:Et quel lien fais-tu entre les entiers de la conjecture de Fermat et les séries ou suites de fonctions convergentes vers 1-(1/e) ?
Je viendrais l'expliquer quand j'aurais atteint une étape significative, cad réussi à montrer la conjecture de Fermat lorsque n tend vers l'infini... :zen:
En tous cas merci pour le tuyau c'est exactement ce que je cherchais ce qui prouve que je suis dans la bonne direction !
-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
 par MacManus » 17 Mai 2012, 14:40
par MacManus » 17 Mai 2012, 14:40
Tu cherches à redémontrer la conjecture de Fermat ?
-
mbj335
- Membre Naturel
- Messages: 13
- Enregistré le: 16 Mai 2012, 12:59
-
 par mbj335 » 17 Mai 2012, 16:52
par mbj335 » 17 Mai 2012, 16:52
MacManus a écrit:Tu cherches à redémontrer la conjecture de Fermat ?
oui, je sais qu'elle a été démontrée mais je suis convaincu qu'il y a une méthode plus simple...enfin on verra !
-
mbj335
- Membre Naturel
- Messages: 13
- Enregistré le: 16 Mai 2012, 12:59
-
 par mbj335 » 17 Mai 2012, 19:27
par mbj335 » 17 Mai 2012, 19:27
mbj335 a écrit:oui, je sais qu'elle a été démontrée mais je suis convaincu qu'il y a une méthode plus simple...enfin on verra !
Je viens de trouver une démonstration par récurrence, elle est tellement simple que je pense avoir fait une erreur, la voici en gros :
Léquation de Fermat peut s'écrire sous cette forme :
On cherche
 E N^3)
tels que
^n+(c-m)^n=c^n)
On s'intéresse aux solutions non nulles donc on a
^{n-1} = Q^c_(n-2))
qui est impossible puisque léquation n'a pas de solution au rang (n-1)
Donc si léquation de Fermat n'a pas de solution au rang (n-1) elle n'en a pas au rang n et comme on sait qu'elle n'en a pas au rang 3, elle n'en a pas à tous les rangs suivants CQFD.
Bien sûr ma seule question sera : où me suis-je planté ? :lol3:
-
mbj335
- Membre Naturel
- Messages: 13
- Enregistré le: 16 Mai 2012, 12:59
-
 par mbj335 » 17 Mai 2012, 20:17
par mbj335 » 17 Mai 2012, 20:17
Bon cette phrase est fausse :
Ce polynôme s'annule pour k=c donc il peut s'écrire sous la forme
*Q^c_(n-2))
ou Q est un polynôme de c de degré n-2.
Quand k=c m=0 et tout c est solution...
-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
 par MacManus » 17 Mai 2012, 20:27
par MacManus » 17 Mai 2012, 20:27
mbj335 a écrit:Bon cette phrase est fausse :
Ce polynôme s'annule pour k=c donc il peut s'écrire sous la forme
*Q^c_(n-2))
ou Q est un polynôme de c de degré n-2.
Quand k=c m=0 et tout c est solution...
c'est bien que tu l'aies vu par toi même !
-
mbj335
- Membre Naturel
- Messages: 13
- Enregistré le: 16 Mai 2012, 12:59
-
 par mbj335 » 17 Mai 2012, 21:25
par mbj335 » 17 Mai 2012, 21:25
Eh oui c'était trop beau ! du coup je vais être obligé de regarder de prêt le fameux polynôme...
mais je trouve l'approche intéressante, complémentaire de celle avec les fonction exponentielle.
A suivre donc...
-
mbj335
- Membre Naturel
- Messages: 13
- Enregistré le: 16 Mai 2012, 12:59
-
 par mbj335 » 18 Mai 2012, 15:15
par mbj335 » 18 Mai 2012, 15:15
Bon la récurrence conduit à une impasse, car elle sous-entend qu'il serait en fait possible d'établir une relation entre les solutions au rang n-1 et celles au rang n :mur:
Retour aux fonctions qui tendent vers 1/e et 1-1/e... :petard:
-
Arkhnor
- Membre Relatif
- Messages: 343
- Enregistré le: 05 Déc 2008, 20:02
-
 par Arkhnor » 18 Mai 2012, 15:20
par Arkhnor » 18 Mai 2012, 15:20
mais je suis convaincu qu'il y a une méthode plus simple
Bah voyons ...
Combien de gens convaincus que le théorème de Fermat peut être démontré simplement inondent les revues mathématiques de leurs "preuves" en trois pages ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 59 invités
n'ont pas de primitives simples donc difficile d'exprimer la limite en fonction de n sans trainer l'intégrale...
