Série non convergente

[Luc]

Pour moi aussi, divergence=non convergence. Mais converger=avoir une limite finie, dont la négation est tendre vers l'infini ou ne pas avoir de limite.

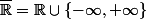
Effectivement, si tu prends la convergence dans . Mais comme les cas d'une limite infinie ne posent pas vraiment de problème, on peut en fait regarder la convergence sur la droite réelle achevée . Dans ce cas là, soit on converge (ie on a une limite, éventuellement infinie), soit on diverge (ie on n'a pas de limite).

[vincentroumezy]

Dans ce cas, bien sûr, diverger<=> ne pas avoir de limite.

[leon1789]

Effectivement, si tu prends la convergence dans .

C'est ce que l'on prend en général.

Mais comme les cas d'une limite infinie ne posent pas vraiment de problème,

hum, ça dépend ce que l'on fait avec les limites... Par exemple, tu sais additionner des infinis opposés ?

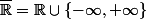
on peut en fait regarder la convergence sur la droite réelle achevée . Dans ce cas là, soit on converge (ie on a une limite, éventuellement infinie), soit on diverge (ie on n'a pas de limite).

Dans ce cas "particulier" de la droite réelle achevée, ok.

[Luc]

hum, ça dépend ce que l'on fait avec les limites... Par exemple, tu sais additionner des infinis opposés ?

Effectivement, on ne peut pas définir la somme , mais on n'en a pas vraiment besoin en fait.

[Sylviel]

En fait suivant les cas on peut effectivement additionner des infini opposé (en définissant la convention). Typiquement en analyse convexe avec pour objectif l'optimisation on a souvent oo-oo = oo.

[asselmarwene]

nous avons une condition nécessaire pour qu'une série converge il faut que son terme général tend vers 0 a l'infini

le terme général de cette série diverge car pour les puissances paires elle vaut 1 et pour les impaires vaut -1