Intégrale
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
ralx
- Membre Naturel
- Messages: 18
- Enregistré le: 15 Mai 2016, 16:04
-
 par ralx » 19 Mai 2016, 11:55
par ralx » 19 Mai 2016, 11:55
Bonjour,
Je souhaiterais calculer l'intégrale suivante

J'ai trouvé le résultat avec un logiciel en ligne mais je ne sais pas comment faire. On trouve :

.
J'ai pensé à dissocier la fraction. On trouve alors facilement l'intégrale de

qui vaut Argshx soit ln(x+
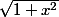
). Pour l'autre terme j'ai pensé à une intégration par parties :

en posant u'=

et v=x ce qui nous donne :

=

- 2.

.
Voilà je suis bloqué en plus je n'arrive pas écrire les expressions mathématiques correctement.
Merci de bien vouloir m'aider.
Modifié en dernier par
ralx le 19 Mai 2016, 12:34, modifié 1 fois.

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 19 Mai 2016, 12:03
par Lostounet » 19 Mai 2016, 12:03
ralx a écrit:Bonjour,
Je souhaiterais calculer la primitive suivante

Hello, tu t'es mis au TEX on dirait

Que penses-tu du changement de variable x = tan(y) ?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
ralx
- Membre Naturel
- Messages: 18
- Enregistré le: 15 Mai 2016, 16:04
-
 par ralx » 19 Mai 2016, 12:35
par ralx » 19 Mai 2016, 12:35
Je vais essayer, pardon je n'avais pas vu ta réponse j'étais encore entrain de modifier mon message.
Ca ressemble à rien snif.

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 19 Mai 2016, 12:43
par zygomatique » 19 Mai 2016, 12:43
salut
x = sinh y devrait être plus efficace ....
sinon remarquer que


Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 19 Mai 2016, 12:55
par Lostounet » 19 Mai 2016, 12:55
Ah oui j'essaye sinh mais j'aboutis très bien avec mon changement de variable aussi!
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
ralx
- Membre Naturel
- Messages: 18
- Enregistré le: 15 Mai 2016, 16:04
-
 par ralx » 19 Mai 2016, 17:09
par ralx » 19 Mai 2016, 17:09
En partant de ta remarque zygomatique j'arrive très bien à calculer l'intégrale.

=

+

. J'intègre par parties

en posant u'=

et v=

.
J'obtiens alors que

=

+

-

=

.
CQFD.Par contre j'aimerais bien que tu m'expliques comment tu es passé de

à
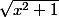
+

. Je vois bien que c'est juste mais je n'arrive pas à passer d'une expression à l'autre.
Pour les deux autres méthodes je me retrouve bloqué.
En posant x=sinh(y) ==> y=argsinh(x) ==> dy=

dx ==>dx=
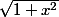
dy.
On a donc

=

=
} \, \mathrm{d}y \])
=y+2.
 \, \mathrm{d}y \])
.Là je sais pas trop quoi faire on s'éloigne de ce que l'on doit trouver.
En posant x=tan(y) ==> dx=(1+tan²(y))dy=(1+x²)dy
On a donc

=
{\sqrt{x^2+1}} \, \mathrm{d}y \])
=
+1)}{\sqrt{tan^2(y)+1}} \, \mathrm{d}y \])
Voilà où j'en suis .
Merci de continuer à m'aider.

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 19 Mai 2016, 17:37
par zygomatique » 19 Mai 2016, 17:37
zygomatique a écrit:salut
x = sinh y devrait être plus efficace ....
sinon remarquer que


quel est l'intérêt de faire une IPP alors qu'on reconnaît immédiatement u'v + uv' ....
pourquoi cette décomposition : parce qu'un
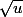
au dénominateur m'amène fortement à penser que j'ai dérivé un
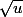
... ensuite ce n'est que du bricolage (propre bien sur)
en remarquant par exemple que 2x² + 1 = x² + x² + 1 et x² + 1 est le carré de sa racine carrée ...

x = sh t => dx = ch t dt et 1 + sh²t = ch t
or ch t > 0 donc
dt = \dfrac 1 2 sh(2t) = ch \ t \ sh \ t = x \sqrt {x^2 + 1})

Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
ralx
- Membre Naturel
- Messages: 18
- Enregistré le: 15 Mai 2016, 16:04
-
 par ralx » 19 Mai 2016, 19:59
par ralx » 19 Mai 2016, 19:59
zygomatique a écrit: zygomatique a écrit:dt = \dfrac 1 2 sh(2t) = ch \ t \ sh \ t = x \sqrt {x^2 + 1})

Je crois qu'il y a une petite erreur à la deuxième étape il ne devrait pas y avoir de terme en sh²t puisque 2sh²t+1=ch(2t). En tout cas le résultat est juste merci.
As-tu une idée de ce qui ne va pas pour mon intégration en posant x=tan(y) ?
Bonne soirée.

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 19 Mai 2016, 22:02
par Lostounet » 19 Mai 2016, 22:02
Hello,
En posant x=tan(y) ==>
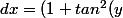)dy=(1+x^2)dy)
Et y = arctan(x)
Notons sec(y) = 1/cos(y). On se ramène, en simplifiant numérateur et dénominateur par

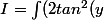 + 1)sec(y)dy)
Rappelons, pour info que tan^2 + 1 = sec^2(y)
Partant de ce constat,
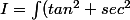sec(y)dy)
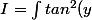.sec(y) + sec^3(y) dy)
Puisque la dérivée de tan(y) est sec^2 et celle de sec est tan.sec on a fini ! On repère la dérivée du produit:
(sec(y).tan(y))' = sec'.tan + tan'.sec = tan^2.sec + sec^3
Finalement:
\times tan(y) = sec(arctan(x)) \times tan(arctan(x)) = x \times \sqrt{x^2 + 1})

Bon désolé c'est assez laborieux finalement... et il faut se souvenir de toutes les formules de trigo. Faisons comme Zygo c'est mieux!
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 20 Mai 2016, 09:48
par zygomatique » 20 Mai 2016, 09:48
je corrige l'erreur : un 2 qui passe en exposant ::
zygomatique a écrit: x = sh t => dx = ch t dt et 1 + sh²t = ch t
or ch t > 0 donc
dt = \dfrac 1 2 sh(2t) = ch \ t \ sh \ t = x \sqrt {x^2 + 1})

Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
ralx
- Membre Naturel
- Messages: 18
- Enregistré le: 15 Mai 2016, 16:04
-
 par ralx » 20 Mai 2016, 12:11
par ralx » 20 Mai 2016, 12:11
Lostounet a écrit:\times tan(y) = sec(arctan(x)) \times tan(arctan(x)) = x \times \sqrt{x^2 + 1})
Pourquoi as-tu retenu le signe + devant la racine (certes c'est la bonne réponse) mais on aurait aussi pu avoir un signe -car
=tan^2+1)
==>
=+/-\sqrt{tan^2+1})
.
Merci.

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 20 Mai 2016, 15:05
par Lostounet » 20 Mai 2016, 15:05
C'est parce que arctan(x) est dans] -pi/2 ; pi/2[ et que cos est positif sur cet intervalle:
1+tan^2(y)=sec^2(y)
Cos^2(y)=1/(1+tan^2(y))
Y=arctan(x)
Cos(arctan(x)) = +-1/V(1+x^2)>0 donc c'est +
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
ralx
- Membre Naturel
- Messages: 18
- Enregistré le: 15 Mai 2016, 16:04
-
 par ralx » 20 Mai 2016, 21:09
par ralx » 20 Mai 2016, 21:09
Ok parfait.
Merci beaucoup pour toutes ces astuces et ces explications.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités


