Bonjour,
Voici l'équation différentielle suivante à résoudre :
y'+(x/1+x²)y=(1+2x²)/(1+x²) (1)
J'ai facilement trouvé la solution de l'équation homogène qui vaut C*(1+x²)^-1/2 mais j'ai mis plus de temps pour trouver la valeur particulière qui s'avère très très simple.J'aimerais donc savoir s'il n'y avait pas une méthode plus rapide vu que c'était une question aux partielles.
Regardez donc ce que j'ai fait :
On cherche yp sous la forme C(x)*(1+x²)-1/2
D'après (1) on a C'(x)*(1+x²)^-1/2 + C(x)*-(x)/((1+x²)*(1+x²)^1/2)+(x*C(x))/(1+x²)*(1+x²)^1/2)=(1+2x²)/(1+x²)
Ce qui nous donne C'(x)=[(1+2x²)(1+x²)^1/2]/(1+x²)=(1+2x²)/(1+x²)^1/2
En m'aidant d'un logiciel j'ai trouvé l'intégrale (ce que je n'ai pas su faire tout seul, j'avais cru reconnaître la forme u'/racine(u) mais l'on a 2x² et pas 2x) et elle vaut x(x²+1)^1/2.
On a donc yp=x*(x²+1)^1/2*(x²+1)^-1/2=x
x est bien solution particulière après vérification.
On a donc y=x+C*(1+x²)^-1/2 avec C constante.
Merci de bien vouloir m'aider,
Cordialement.
PS : Comment fait-on pour écrire lisiblement ses calculs avec les traits de fractions, les racines... ?
Dois-je créer un autre sujet pour l'intégrale qui m'a posée problème.
Equation différentielle d'ordre 1.
6 messages
- Page 1 sur 1
Re: Equation différentielle d'ordre 1.
Puisque  l'équation s'écrit
l'équation s'écrit y'+xy=1+2x^2) et on voit tout de suite que
et on voit tout de suite que 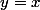 est solution particulière.
est solution particulière.
Re: Equation différentielle d'ordre 1.
Merci beaucoup c'est sûrement ce que l'on attendait de nous.
Une idée pour l'intégrale ?
Une idée pour l'intégrale ?
Re: Equation différentielle d'ordre 1.
ralx a écrit:
PS : Comment fait-on pour écrire lisiblement ses calculs avec les traits de fractions, les racines... ?
Dois-je créer un autre sujet pour l'intégrale qui m'a posée problème.
Regarde ici: guide-utilisation-f41/ecrire-des-belles-formules-mathematiques-balises-tex-t70548.html
Oui c'est mieux de créer un nouveau sujet pour une nouvelle question !
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Equation différentielle d'ordre 1.
De rien, si tu as d'autres questions n'hésite pas !
Puisque tu es nouveau, tu devrais faire un tour dans la section 'Guide d'Utilisation'
Ps: Tu ne t'es pas encore présenté tu as la possibilité de te faire connaitre dans la section 'Présentez-vous'
tu as la possibilité de te faire connaitre dans la section 'Présentez-vous'
Puisque tu es nouveau, tu devrais faire un tour dans la section 'Guide d'Utilisation'
Ps: Tu ne t'es pas encore présenté
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
