Exercice de spé

par **neil77** » 03 Oct 2006, 22:19

1° soit d,k,k' des entiers relatifs vérifiant d= 5k et d=2k' . Vérifier que d= 10(k'-2k)
2° soit n appartenant à N*
a) montrer que n( n^4 -1) est divisible par 2
b) montrer que n(n^4 -1) est divisible par 5
c) en déduire que n(n^4 -1) est divisible par 10
3° démontrer que, pour tout nombre p appartenant à N* les nombres n puissance p et n puissance p+4 ont le même chiffre des unités.

Voila j'ai fait toutes les kestion sauf sur la 3 où je bloque. Merci pour votre aide...

par **matteo182** » 03 Oct 2006, 22:23

Salut,
Utilise la congruence modulo 10.

par **neil77** » 03 Oct 2006, 22:31

oui je sais j'y est pensais mais je me perds vraiment dans mon raisonnement. Je ne sais pas par quoi commencer

par **allomomo** » 03 Oct 2006, 22:39

Salut,

a /

Les restes possibles dans la division euclidiènne de n par 2 sont 0,1. donc n s'écrit de l'une des façons suivantes :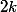

ou

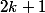avec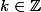

1er cas :

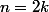. Alors 2 divise n et donc 2 divise

2eme cas :

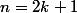. Alors

Les deux cas permettent de conclure que pour tout entier relatif n, 2 divise n(n^4-1).

PAreil pour les autres ...

Remarque : il y a des methodes bcq plus rapides .. mais je pense que c'est ca que tu dois faire (puis que c'est la divisibilité)

par **matteo182** » 03 Oct 2006, 22:41

Il faut que tu montres que

et

sont congrus au même nombre modulo 10.
Pour ca il faut écrire

et

de manière différente, ce qui te permettra d'utiliser les questions précédentes.

par **neil77** » 03 Oct 2006, 22:42

Je ne vois pas comment transformer n^p

par **allomomo** » 03 Oct 2006, 22:42

Une remarque qui n'a pas forcément de rapport ici,

Ici par exemple on pourrait dire directement que ca divise 3.

par **neil77** » 03 Oct 2006, 23:02

J'ai prouvé que n^p et n^(p+4) sont congrus à 0 modulo 10 mais parès je ne sais plus quoi faire...

Exercice de spé

Exercice de spé

Qui est en ligne