SUite
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Lalyo
- Membre Naturel
- Messages: 30
- Enregistré le: 09 Sep 2006, 09:02
-
 par Lalyo » 03 Oct 2006, 18:26
par Lalyo » 03 Oct 2006, 18:26
bonjour a tous, voila j'ai un ptit probleme de maths ^
ça serait sympa de m'aider svp
On injecte par piqure intraveineuse, une dose de 1.5 unité d'une substance médicamenteuse dans le sang à l'instant t=0 ( t est exprimé en heures)
On sait que sur une période quelquonque d'une heure la quantité de substance présente dans le sang diminue de 20%. On décide alors de réinjecter une dose compensatrice de 1.5 unité à l'instant t=1 ( au bout d'une heure ) puis aux instants t=2, t=3, etc.
On note An la quantité de substance présente dans le sang à l'instant t=n dès que la nouvelle injection est faite. Donc Ao = 1.5
a) Montrer que A1= 1.5 + 0.8 x 1.5. Calculer A2.
b) Exprimer An+1 en fonction de An
c) Soit la suite ( Bn ) définie par
Bn= An-7.5 . Démontrer que ( Bn ) est une suite géométrique et en déduire l'expression de An en fonction de n
d)Déterminer la limite de la suite
v'la je suis a la b) mais je vois pas quel expresion ca peut donner,
merci a tte les ames charitable de ce forums ^^
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 03 Oct 2006, 18:31
par Zebulon » 03 Oct 2006, 18:31
Bonsoir,
au temps t=n, il reste 80% de la quantité qu'il y avait au temps n-1, et on y ajoute une quantité de 1.5. Quelle est donc l'expression de

en fonction de

?
-
Lalyo
- Membre Naturel
- Messages: 30
- Enregistré le: 09 Sep 2006, 09:02
-
 par Lalyo » 03 Oct 2006, 18:34
par Lalyo » 03 Oct 2006, 18:34
An+1 = 1.5 + 0.8*An je crois que ca donne ca !!
mais apres je bloque au autre question !!!
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 03 Oct 2006, 18:39
par Zebulon » 03 Oct 2006, 18:39
OK pour l'expression de

!
Ensuite, pour montrer que
)
est une suite géométrique, il suffit de montrer qu'il existe un certain réel k tel que

.
On commence par exprimer
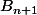
:

d'après l'expression de
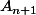
. Donc
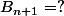
-
Lalyo
- Membre Naturel
- Messages: 30
- Enregistré le: 09 Sep 2006, 09:02
-
 par Lalyo » 03 Oct 2006, 18:58
par Lalyo » 03 Oct 2006, 18:58
c'est 0.8 non ??
oué mais apres pour l'expresion de An en fonction de n, je fais comment ??
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 03 Oct 2006, 19:04
par Zebulon » 03 Oct 2006, 19:04
Lalyo a écrit:c'est 0.8 non ??
Qu'est-ce qui est 0.8?
Une fois qu'on a l'expression de
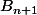
en fonction de

, on met en évidence que
)
est une suite géométrique. On en déduit alors l'expression de

en fonction de n, et comme
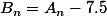
, on en déduit l'expression de

en fonction de n.
-
Lalyo
- Membre Naturel
- Messages: 30
- Enregistré le: 09 Sep 2006, 09:02
-
 par Lalyo » 03 Oct 2006, 19:09
par Lalyo » 03 Oct 2006, 19:09
oki
le 0.8 c'est ca : Bn+1/Bn = (An+1 - 7.5)/(An - 7.5) = (0.8An - 6)/(An - 7.5) = 0.8(An - 7.5)/(An - 7.5) = 0.8
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 03 Oct 2006, 19:15
par Zebulon » 03 Oct 2006, 19:15
OK. Et donc quelle est l'expression de

en fonction de n?
-
Lalyo
- Membre Naturel
- Messages: 30
- Enregistré le: 09 Sep 2006, 09:02
-
 par Lalyo » 03 Oct 2006, 19:22
par Lalyo » 03 Oct 2006, 19:22
je vois pas...
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 03 Oct 2006, 19:30
par Zebulon » 03 Oct 2006, 19:30
C'est du cours!
Soit
_{n\geq0})
une suite géométrique de raison q et de premier terme

. Alors pour tout
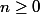
,
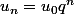
. Ce qui donne pour

?
-
Lalyo
- Membre Naturel
- Messages: 30
- Enregistré le: 09 Sep 2006, 09:02
-
 par Lalyo » 03 Oct 2006, 19:34
par Lalyo » 03 Oct 2006, 19:34
Bn= 1.5*(0.8)^n ??
je suis pas sur de ca...
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 03 Oct 2006, 19:43
par Zebulon » 03 Oct 2006, 19:43
-
Lalyo
- Membre Naturel
- Messages: 30
- Enregistré le: 09 Sep 2006, 09:02
-
 par Lalyo » 03 Oct 2006, 19:45
par Lalyo » 03 Oct 2006, 19:45
Bn= -6*(0.8)^n ??
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 03 Oct 2006, 19:51
par Zebulon » 03 Oct 2006, 19:51
Oui, c'est bien ça. Quelle est donc l'expression de

en fonction de n?
-
Lalyo
- Membre Naturel
- Messages: 30
- Enregistré le: 09 Sep 2006, 09:02
-
 par Lalyo » 03 Oct 2006, 19:52
par Lalyo » 03 Oct 2006, 19:52
An = Bn + 7.5 ??
j'ai une autre question c'est quoi la limite de la suite a ??
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 03 Oct 2006, 20:00
par Zebulon » 03 Oct 2006, 20:00
Oui, ce qui donne pour

en fonction de n?
-
Lalyo
- Membre Naturel
- Messages: 30
- Enregistré le: 09 Sep 2006, 09:02
-
 par Lalyo » 03 Oct 2006, 20:03
par Lalyo » 03 Oct 2006, 20:03
et An= -6*(0.8)^n+7.5
et pour la limite on doir trouver quoi ?
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 03 Oct 2006, 20:07
par Zebulon » 03 Oct 2006, 20:07
Quelle est la limite de la suite des
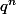
avec q<1?
-
Lalyo
- Membre Naturel
- Messages: 30
- Enregistré le: 09 Sep 2006, 09:02
-
 par Lalyo » 03 Oct 2006, 20:14
par Lalyo » 03 Oct 2006, 20:14
An = 7.5 - 6*(0.8)^n
Quand n tend vers l´infini, 0.8^n tend vers 0, donc An tend vers 7.5 .
j'espere que c'est ca !!!
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 03 Oct 2006, 20:18
par Zebulon » 03 Oct 2006, 20:18
C'est ça! :++:
Bonne soirée et à bientôt!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 79 invités
