Exercice sur les dérivées (t°S)
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
dodi
- Membre Naturel
- Messages: 49
- Enregistré le: 08 Mai 2006, 13:33
-
 par dodi » 03 Oct 2006, 17:53
par dodi » 03 Oct 2006, 17:53
bonjour j'ai un petit problème sur un exercice:
"On veut montrer que: quelque soit x> ou = 0 x - sinxPour cela on considère µ(x)=sinx - x + x^3/6.Calculer les dérivées successives µ' , µ'' et µ''' de µ et en déduire le signe de µ.
Conclure."
J'ai trouvé les dérivées successives:
µ'(x)=cosx - 1 + 3x/6
µ''(x)=-sinx + 1/2
µ'''(x)=cosx
mais je ne vois pas du tout comment en déduire le signe de µ
merci de bien vouloir me donner un petit coup de pouce
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 03 Oct 2006, 18:07
par Zebulon » 03 Oct 2006, 18:07
Bonsoir,
on veut montrer que
\leq{x^3\over6})
.
On introduit

, définie sur [0,+

[ par
=sin(x)-x+{x^3\over6})
.
On veut étudier le signe de

.
On commence par calculer les dérivées successives de

. Vous avez fait une erreur à
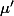
: la dérivée de

est

.
Je vous laisse recalculer les dérivées. Essayez aussi de mmontrer pourquoi, si on arrive à démontrer que

est positive sur [0,+

[, on a montré que
\leq{x^3\over6})
.
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 03 Oct 2006, 18:15
par fonfon » 03 Oct 2006, 18:15
Salut zeb, oulala ça faisait un bail :we:
-
dodi
- Membre Naturel
- Messages: 49
- Enregistré le: 08 Mai 2006, 13:33
-
 par dodi » 03 Oct 2006, 18:36
par dodi » 03 Oct 2006, 18:36
pourquoi la dérivée de x^3/6 est égale a x²/6?
parce que dans ma logique, x^3/6 = x^3 * 1/6 dc (x^3/6)'=3x * 1/6=3x/6
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 03 Oct 2006, 18:40
par Zebulon » 03 Oct 2006, 18:40
Quelle est la dérivée de

pour n entier?
-
dodi
- Membre Naturel
- Messages: 49
- Enregistré le: 08 Mai 2006, 13:33
-
 par dodi » 03 Oct 2006, 18:44
par dodi » 03 Oct 2006, 18:44
c'est n*x^n-1
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 03 Oct 2006, 18:53
par Zebulon » 03 Oct 2006, 18:53
OK. Alors, pour n=3, ça fait...?
-
dodi
- Membre Naturel
- Messages: 49
- Enregistré le: 08 Mai 2006, 13:33
-
 par dodi » 03 Oct 2006, 19:12
par dodi » 03 Oct 2006, 19:12
a oui j'ai oublié la puissance donc effectivement ça fait 3x² désolée
-
dodi
- Membre Naturel
- Messages: 49
- Enregistré le: 08 Mai 2006, 13:33
-
 par dodi » 03 Oct 2006, 19:14
par dodi » 03 Oct 2006, 19:14
donc on trouve µ'=cosx-1+x²/2
µ''=-sinx+2x
µ'''=cosx+1
c'est ça?
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 03 Oct 2006, 19:17
par Zebulon » 03 Oct 2006, 19:17
dodi a écrit:donc on trouve µ'=cosx-1+x²/2
µ''=-sinx+2x
µ'''=cosx+1
c'est ça?
Il y a une erreur à

' :
quelle est la dérivée de

?
-
dodi
- Membre Naturel
- Messages: 49
- Enregistré le: 08 Mai 2006, 13:33
-
 par dodi » 03 Oct 2006, 19:20
par dodi » 03 Oct 2006, 19:20
oui ça fait x pardon c'est juste une erreur de frappe
-
babaz
- Membre Naturel
- Messages: 71
- Enregistré le: 30 Aoû 2006, 15:07
-
 par babaz » 03 Oct 2006, 19:24
par babaz » 03 Oct 2006, 19:24
Zebulon a écrit:Essayez aussi de mmontrer pourquoi, si on arrive à démontrer que

est positive sur [0,+

[, on a montré que
\leq{x^3\over6})
.
Reste à faire.
-
dodi
- Membre Naturel
- Messages: 49
- Enregistré le: 08 Mai 2006, 13:33
-
 par dodi » 03 Oct 2006, 19:27
par dodi » 03 Oct 2006, 19:27
si sinx-x+x^3/6>ou=0
alors sinx-x>ou=-x^3/6
donc x-sinxou=0
c'est bon comme raisonnement?
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 03 Oct 2006, 19:32
par Zebulon » 03 Oct 2006, 19:32
Oui, c'est bon. Maintenant montrez que pour tout
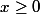
,
\geq0)
et le tour est joué...
-
dodi
- Membre Naturel
- Messages: 49
- Enregistré le: 08 Mai 2006, 13:33
-
 par dodi » 03 Oct 2006, 19:39
par dodi » 03 Oct 2006, 19:39
je trouve que µ'''(x)>ou=0 en partant d'un encadrement
et que µ''(x)>ou=0 en partant pareil d'un encadrement mais je voit pas comment on peut relier toutes les dérivées afin de trouver le signe de µ
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 03 Oct 2006, 19:50
par Zebulon » 03 Oct 2006, 19:50
Pour les dérivées, je trouve
=cos(x)-1+{x^2\over2})
,
=-sin(x)+x)
et
=-cos(x)+1)
.
Comme pour tout
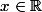
\leq1)
, pour tout
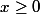
\geq0)
donc

est croissante sur [0,+

[. Or
=0)
donc pour tout
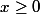
,
\geq0)
. Déduisez-en les variations de
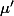
, puis son signe. Déduisez-en les variations de

puis le signe de

.
-
dodi
- Membre Naturel
- Messages: 49
- Enregistré le: 08 Mai 2006, 13:33
-
 par dodi » 03 Oct 2006, 20:04
par dodi » 03 Oct 2006, 20:04
pour tout x E R cox(x)ou=0 µ'''(x)>ou=0 donc µ''(x) est croissante sur ]o;+l'infini[
or µ''(0)=0 donc pour tout x>ou=0, µ''(x)>ou=0
donc µ'(x) est croissante sur ]0;+l'infini[
or µ'(0)=0 donc pour tout x>ou=0 µ'(x)>ou=0
donc µ(x) est croissante sur ]0;+l'infini[
or µ(0)=1 donc µ(x)>ou=0
donc sinx-x+x^3/6>ou=0
donc sinx-x>ou=x^3/6
donc x-sinxet voilà fin de l'exercice
c'est juste?
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 03 Oct 2006, 20:10
par Zebulon » 03 Oct 2006, 20:10
C'est presque bon :
les intervalles sont fermés en 0 : [0,+

[ et
=0)
. Mais à part ça, c'est tout bon! :happy2:
-
dodi
- Membre Naturel
- Messages: 49
- Enregistré le: 08 Mai 2006, 13:33
-
 par dodi » 03 Oct 2006, 20:25
par dodi » 03 Oct 2006, 20:25
oki merci beaucoup beaucoup beaucoup bisous
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 03 Oct 2006, 20:26
par Zebulon » 03 Oct 2006, 20:26
Bonne soirée et à bientôt!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 69 invités
