Bonjour à tous alors voilà, j'ai un DM de maths à rendre pour dans une semaine sur les probabilités et je n'y arrive vraiment pas, voici l'énoncé :
"On considère une variable aléatoire X suivant une loi binomiale telle que E(X) = 1 et 4P(X=0) = 3P(X=1) ; on suppose de plus que P(X=0) est différent de 0.
1) Déterminer les paramètres de la loi binomiale suivie par X
2) Calculer alors p(X=2) "
Pour la première question je sais que E(X) = N x P mais je ne vois vraiment pas comment les calculer avec ce qui nous est donné... Merci d'avance !
Probabilités
11 messages
- Page 1 sur 1
Re: probabilités
Salut,
Si X suit une loi binomiale de paramètres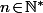 et
et  , c'est combien la proba que X=0 ? (en fonction de
, c'est combien la proba que X=0 ? (en fonction de  et
et  bien sûr)
bien sûr)
Et la proba que X=1 ?
Si X suit une loi binomiale de paramètres
Et la proba que X=1 ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: probabilités
C'est tout bon (mais ça serait pas con de simplifier un peu...)
Ensuite l'énoncé te dit que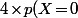=3\!\times\! p(X\!=\!1)) ce qui signifie que ...
ce qui signifie que ...
Et avec la première relation que tu as trouvé, à savoir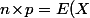=1) , ça te fait deux équations et deux inconnues (
, ça te fait deux équations et deux inconnues ( et
et  ) : ça devrait pas trop mal se goupiller...
) : ça devrait pas trop mal se goupiller...
Ensuite l'énoncé te dit que
Et avec la première relation que tu as trouvé, à savoir
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: probabilités
d'accord donc en simplifiant j'obtiens :
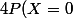 = 4(1-p)^{n-0}) et
et 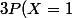=3 n (1-p)^{n-1})
donc j'ai^{n-0}) =
=^{n-1})
et c'est là que je ne vois pas comment résoudre l'équation..
donc j'ai
et c'est là que je ne vois pas comment résoudre l'équation..
Re: probabilités
marianne a écrit:d'accord donc en simplifiant j'obtiens :et
<-
, ça vaut
donc j'ai=
1) Ne pourrait on pas diviser des deux cotés par ... (est-il non nul ?) pour simplifier ?
2) Tu as aussi une autre équation qui te dit que
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: probabilités
Je peux simplifier par (1-p)^n ?
Mais ensuite je trouve
4x(1-p)^n-0 =3.n.p. (1-p)^n-1
4 = 3.n.p.-1
4=3.1.-1 ?
C'est bizarre
Mais ensuite je trouve
4x(1-p)^n-0 =3.n.p. (1-p)^n-1
4 = 3.n.p.-1
4=3.1.-1 ?
C'est bizarre
Re: probabilités
Si tu divise des deux cotés par ^n) alors, du coté où il y avait
alors, du coté où il y avait ^n) , ça va évidement faire 1.
, ça va évidement faire 1.
Mais du coté où il y avait^{n-1}) , ça fait surement pas 1 vu que avait
, ça fait surement pas 1 vu que avait ^{n-1}\!\not=\!(1\!-\!p)^n) .
.
Ca fait combien ?
?
Autre problème : a-t-on le droit de diviser des deux cotés par^n) ? Pourquoi ?
? Pourquoi ?
Mais du coté où il y avait
Ca fait combien
Autre problème : a-t-on le droit de diviser des deux cotés par
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: probabilités
( X^n-1 ) / X^n = X^n-1-n = X ^ -1 ?
Sinon je ne vois toujours pas comment simplifier...
Sinon je ne vois toujours pas comment simplifier...
Re: probabilités
marianne a écrit:( X^n-1 ) / X^n = X^n-1-n = X ^ -1 ?
Sinon je ne vois toujours pas comment simplifier...
salut
s'écrit
Factorise
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 73 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
